Testing population proportions

Available under Creative Commons-ShareAlike 4.0 International License.

As you learned in the chapter “Making estimates”, sample proportions can be used to compute a statistic that has a known sampling distribution. Reviewing, the z-statistic is:

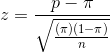
$z=\frac{p-\pi}{\sqrt{\frac{(\pi)(1-\pi)}{n}}}$

where: p = the proportion of the sample with a certain characteristic
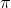$\pi$ = the proportion of the population with that characteristic.

These sample z-statistics are distributed normally, so that by using the bottom line of the t table, you can find what portion of all samples from a population with a given population proportion, 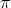$\pi$ , have z-statistics within different ranges. If you look at the table, you can see that .95 of all samples from any population have a z-statistics between ±1.96, for instance.

If you have a sample that you think is from a population containing a certain proportion, 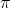$\pi$ , of members with some characteristic, you can test to see if the data in your sample supports what you think. The basic strategy is the same as that explained earlier in this chapter and followed in the "goodness-of-fit" example: (a) write two hypotheses, (b) find a sample statistic and sampling distribution that will let you develop a decision rule for choosing between the two hypotheses, and (c) compute your sample statistic and choose the hypothesis supported by the data.

Foothill Hosiery recently received an order for children's socks decorated with embroidered patches of cartoon characters. Foothill did not have the right machinery to sew on the embroidered patches and contracted out the sewing. While the order was filled and Foothill made a profit on it, the sewing contractor's price seemed high, and Foothill had to keep pressure on the contractor to deliver the socks by the date agreed upon. Foothill's CEO, John McGrath has explored buying the machinery necessary to allow Foothill to sew patches on socks themselves. He has discovered that if more than a quarter of the children's socks they make are ordered with patches, the machinery will be a sound investment. Mr. McGrath asks Kevin Schmidt to find out if more than 25 per cent of children's socks are being sold with patches.

Kevin calls the major trade organizations for the hosiery, embroidery, and children's clothes industries, and no one can answer his question. Kevin decides it must be time to take a sample and to test to see if more than 25 per cent of children's socks are decorated with patches. He calls the sales manager at Foothill and she agrees to ask her salespeople to look at store displays of children's socks, counting how many pairs are displayed and how many of those are decorated with patches. Two weeks later, Kevin gets a memo from the sales manager telling him that of the 2,483 pairs of children's socks on display at stores where the salespeople counted, 716 pairs had embroidered patches.

Kevin writes his hypotheses, remembering that Foothill will be making a decision about spending a fair amount of money based on what he finds. To be more certain that he is right if he recommends that the money be spent, Kevin writes his hypotheses so that the "unusual" world would be the one where more than 25 per cent of children's socks are decorated:

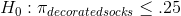
$H_{0}:\pi_{decorated socks}\leq .25$

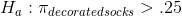
$H_{a}:\pi_{decorated socks}> .25$

When writing his hypotheses, Kevin knows that if his sample has a proportion of decorated socks well below .25, he will want to recommend against buying the machinery. He only wants to say the data supports the alternative if the sample proportion is well above .25. To include the low values in the null hypothesis and only the high values in the alternative, he uses a "one-tail" test, judging that the data supports the alternative only if his z-score is in the upper tail. He will conclude that the machinery should be bought only if his z-statistic is too large to have easily have come from the sampling distribution drawn from a population with a proportion of .25. Kevin will accept H_a : only if his z is large and positive.

Checking the bottom line of the t-table, Kevin sees that .95 of all z-scores are less than 1.645. His rule is therefore to conclude that his sample data supports the null hypothesis that 25 per cent or less of children's socks are decorated if his sample z is less than 1.645. If his sample z is greater than 1.645, he will conclude that more than 25 per cent of children's socks are decorated and that Foothill Hosiery should invest in the machinery needed to sew embroidered patches on socks.

Using the data the salespeople collected, Kevin finds the proportion of the sample that is decorated:

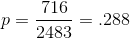
$p=\frac{716}{2483}=.288$

Using this value, he computes his sample z-statistic:

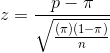
$z=\frac{p-\pi}{\sqrt{\frac{(\pi)(1-\pi)}{n}}}$

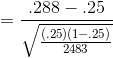
$=\frac{.288-.25}{\sqrt{\frac{(.25)(1-.25)}{2483}}}$

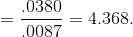
$=\frac{.0380}{.0087}=4.368.$

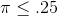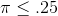Because his sample z-score is larger than 1.645, it is unlikely that his sample z came from the sampling distribution of z's drawn from a population where $\pi\leq .25$ , so it is unlikely that his sample comes from a population with $\pi\leq .25$ . Kevin can tell John McGrath that the sample the sales people collected supports the conclusion that more than 25 per cent of children's socks are decorated with embroidered patches. John can feel comfortable making the decision to buy the embroidery and sewing machinery.

931 reads

You are here

Testing population proportions