Correlation and covariance

Available under Creative Commons-ShareAlike 4.0 International License.

The correlation between two variables is important in statistics, and it is commonly reported. What is correlation? The meaning of correlation can be discovered by looking closely at the word—it is almost co-relation, and that is what it means: how two variables are co-related. Correlation is also closely related to regression. The covariance between two variables is also important in statistics, but it is seldom reported. Its meaning can also be discovered by looking closely at the word—it is co-variance, how two variables vary together. Covariance plays a behind-the-scenes role in multivariate statistics. Though you will not see covariance reported very often, understanding it will help you understand multivariate statistics like understanding variance helps you understand univariate statistics.

There are two ways to look at correlation. The first flows directly from regression and the second from covariance. Since you just learned about regression, it makes sense to start with that approach.

Correlation is measured with a number between -1 and +1 called the correlation coefficient. The population correlation coefficient is usually written as the Greek "rho", 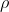$\rho$ , and the sample correlation coefficient as r. If you have a linear regression equation with only one explanatory variable, the sign of the correlation coefficient shows whether the slope of the regression line is positive or negative, while the absolute value of the coefficient shows how close to the regression line the points lie. 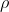If $\rho$ is +.95, then the regression line has a positive slope and the points in the population are very close to the regression line. If r is -.13 then the regression line has a negative slope and the points in the sample are scattered far from the regression line. If you square r, you will get R², which is higher if the points in the sample lie very close to the regression line so that the sum of squares regression is close to the sum of squares total.

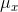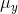The other approach to explaining correlation requires understanding covariance, how two variables vary together. Because covariance is a multivariate statistic it measures something about a sample or population of observations where each observation has two or more variables. Think of a population of (x,y) pairs. First find the mean of the x's and the mean of the y's, $\mu _{x}$ and $\mu _{y}$ . 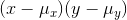Then for each observation, find $(x-\mu_{x})(y-\mu_{y})$ . If the x and the y in this observation are both far above their means, then this number will be large and positive. If both are far below their means, it will also be large and positive. 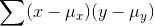If you found $\sum (x-\mu_{x})(y-\mu_{y})$ , it would be large and positive if x and y move up and down together, so that large x's go with large y's, small x's go with small y's, and medium x's go with medium y's. However, if some of the large x's go with medium y's, etc. then the sum will be smaller, though probably still positive. 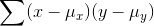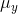A $\sum (x-\mu_{x})(y-\mu_{y})$ implies that x's above x are generally paired with y's above $\mu _{y}$ , and those x's below their mean are generally paired with y's below their mean. As you can see, y the sum is a measure of how x and y vary together. The more often similar x's are paired with similar y's, the more x and y vary together and the larger the sum and the covariance.

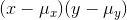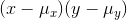The term for a single observation, $(x-\mu_{x})(y-\mu_{y})$ , will be negative when the x and y are on opposite sides xy of their means. If large x's are usually paired with small y's, and vice-versa, most of the terms will be negative and the sum will be negative. If the largest x's are paired with the smallest y's and the smallest x's with the largest y's, then many of the $(x-\mu_{x})(y-\mu_{y})$ will be large and negative and so will the sum. A population with more xy members will have a larger sum simply because there are more terms to be added together, so you divide the sum by the number of observations to get the final measure, the covariance, or cov:

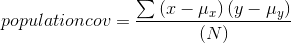
$population cov=\frac{\sum \left ( x-\mu _{x} \right )\left ( y-\mu _{y} \right )}{\left ( N \right )}$

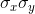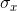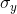The maximum for the covariance is the product of the standard deviations of the x values and of the y values, $\sigma _{x}\sigma _{y}$ . While proving that the maximum is exactly equal to the product of the standard deviations is complicated, you should be able to see that the more spread out the points are, the greater the covariance can be. By now you should understand that a larger standard deviation means that the points are more spread out, so you should understand that a larger $\sigma _{x}$ or a larger $\sigma _{y}$ will allow for a greater covariance.

Sample covariance is measured similarly, except the sum is divided by n-1 so that sample covariance is an unbiased estimator of population covariance:

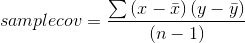
$samplecov=\frac{\sum \left ( x-\bar{x} \right )\left ( y-\bar{y} \right )}{\left ( n-1 \right )}$

Correlation simply compares the covariance to the standard deviations of the two variables. Using the formula for population correlation:

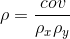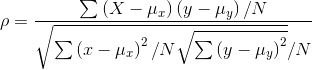
$\rho =\frac{cov}{\rho _{x}\rho _{y}}$ or $\rho =\frac{\sum \left ( X-\mu _{x} \right )\left ( y-\mu _{y} \right )/ N}{\sqrt{\sum \left ( x-\mu _{x} \right )^{2}/ N\sqrt{\sum\left ( y-\mu _{y} \right )^{2} }}/ N}$

At its maximum, the absolute value of the covariance equals the product of the standard deviations, so at its maximum, the absolute value of r will be 1. Since the covariance can be negative or positive while standard deviations are always positive, r can be either negative or positive. Putting these two facts together, you can see that r will be between -1 and +1. The sign depends on the sign of the covariance and the absolute value depends on how close the covariance is to its maximum. The covariance rises as the relationship between x and y grows stronger, so a strong relationship between x and y will result in r having a value close to -1 or +1.

1757 reads

You are here

Correlation and covariance