Before starting to learn about regression, go back to algebra and review what a function is. The definition of a function can be formal, like the one in my freshman calculus text: "A function is a set of ordered pairs of numbers (x,y) such that to each value of the first variable (x) there corresponds a unique value of the second variable (y)". 1 More intuitively, if there is a regular relationship between two variables, there is usually a function that describes the relationship. Functions are written in a number of forms. The most general is "y = f(x)", which simply says that the value of y depends on the value of x in some regular fashion, though the form of the relationship is not specified. The simplest functional form is the linear function where
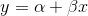
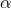 and
and 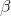 are parameters, remaining constant as x and y change.
are parameters, remaining constant as x and y change. 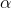 is the intercept and
is the intercept and 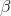 is the slope. If the values of and are known, you can find the y that goes with any x by putting the x into the equation and
solving. There can be functions where one variable depends on the values of two or more other variables:
is the slope. If the values of and are known, you can find the y that goes with any x by putting the x into the equation and
solving. There can be functions where one variable depends on the values of two or more other variables:
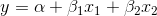
where x1 and x2 together determine the value of y. There can also be non-linear functions, where the value of the dependent variable ("y" in all of the examples we have used so far) depends on the values of one or more other variables, but the values of the other variables are squared, or taken to some other power or root or multiplied together, before the value of the dependent variable is determined. Regression allows you to estimate directly the parameters in linear functions only, though there are tricks which allow many non-linear functional forms to be estimated indirectly. Regression also allows you to test to see if there is a functional relationship between the variables, by testing the hypothesis that each of the slopes has a value of zero.
First, let us consider the simple case of a two variable function. You believe that y, the dependent variable, is a linear function of x, the independent variable—y depends on x. Collect a sample of (x, y) pairs, and plot them on a set of x, y axes. The basic idea behind regression is to find the equation of the straight line that "comes as close as possible to as many of the points as possible". The parameters of the line drawn through the sample are unbiased estimators of the parameters of the line that would "come as close as possible to as many of the point as possible" in the population, if the population had been gathered and plotted. In keeping with the convention of using Greek letters for population values and Roman letters for sample values, the line drawn through a population is
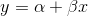
while the line drawn through a sample is
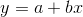
In most cases, even if the whole population had been gathered, the regression line would not go through every point. Most of the phenomena that business researchers deal with are not perfectly deterministic, so no function will perfectly predict or explain every observation.
Imagine that you wanted to study household use of laundry soap. You decide to estimate soap use as a function of family size. If you collected a large sample of (family size, soap use) pairs
you would find that different families of the same size use different amounts of laundry soap—there is a distribution of soap use at each family size. When you use regression to estimate the
parameters of soap use = f(family size), you are estimating the parameters of the line that connects the mean soap use at each family size. Because the best that can be expected is to predict
the mean soap use for a certain size family, researchers often write their regression models with an extra term, the "error term", which notes that many of the members of the population of
(family size, soap use) pairs will not have exactly the predicted soap use because many of the points do not lie directly on the regression line. The error term is usually denoted as " ", or "epsilon", and you often see regression equations written
", or "epsilon", and you often see regression equations written
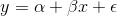
Strictly, the distribution of  at each family size must be
normal, and the distributions of
at each family size must be
normal, and the distributions of  for all of the family sizes
must have the same variance (this is known as homoskedasticity to statisticians).
for all of the family sizes
must have the same variance (this is known as homoskedasticity to statisticians).
It is common to use regression to estimate the form of a function which has more than one independent, or explanatory, variable. If household soap use depends on household income as well as family size, then soap use = f(family size, income), or
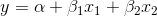
where y is soap use, x1 is family size and x2 is income. This is the equation for a plane, the three-dimensional equivalent of a straight line. It is still a linear
function because neither of the x's nor y is raised to a power nor taken to some root nor are the x's multiplied together. You can have even more independent variables, and as long as the
function is linear, you can estimate the slope, 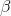 , for each
independent variable.
, for each
independent variable.
- 1588 reads






