There are many times when you, or your boss, will want to estimate the proportion of a population that has a certain characteristic. The best known examples are political polls when the proportion of voters who would vote for a certain candidate is estimated. This is a little trickier than estimating a population mean. It should only be done with large samples and there are adjustments that should be made under various conditions. We will cover the simplest case here, assuming that the population is very large, the sample is large, and that once a member of the population is chosen to be in the sample, it is replaced so that it might be chosen again. Statisticians have found that, when all of the assumptions are met, there is a sample statistic that follows the standard normal distribution. If all of the possible samples of a certain size are chosen, and for each sample, p, the proportion of the sample with a certain characteristic, is found, and for each sample a z-statistic is computed with the formula:
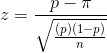
where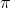 
= proportion of population with the characteristic these will
be distributed normally. Looking at the bottom line of the t-table, .90 of these z's will be between ±1.645, .99 will be between ±2.326, etc.
Because statisticians know that the z-scores found from sample will be distributed normally, you can make an interval estimate of the proportion of the population with the characteristic. This
is simple to do, and the method is parallel to that used to make an interval estimate of the population mean: (1) choose the sample, (2) find the sample p, (3) assume that your sample has a
z-score that is not in the tails of the sampling distribution, (4) using the sample p as an estimate of the population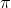 
in the denominator and the table z-values for the desired level of confidence, solve twice to find the limits of the interval that
you believe contains the population proportion, p.
At Foothill Hosiery, Ann Howard is also asked by John McGrath to look into the age at hiring at the plant. Ann takes a different approach than Kevin, and decides to investigate what proportion of new hires were at least 35. She looks at the personnel records and, like Kevin, decides to make an inference from a sample after finding that over 2,500 different people have worked at Foothill at some time in the last fifteen years. She chooses 100 personnel files, replacing each file after she has recorded the age of the person at hiring. She finds 17 who were 35 or older when they first worked at Foothill. She decides to make her inference with .95 confidence, and from the last line of the t-table finds that .95 of z-scores lie between ±1.96. She finds her upper and lower bounds:
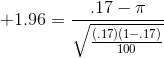
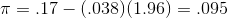
and, she finds the other boundary:
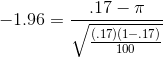
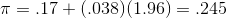
and concludes, that with .95 confidence, the proportion of people who have worked at Foothills Hosiery who were over 35 when hired is between .095 and .245. This is a fairly wide interval. Looking at the equation for constructing the interval, you should be able to see that a larger sample size will result in a narrower interval, just as it did when estimating the population mean.
- 905 reads
