Measuring the location of a sample is done in exactly the way that the location of a population is done. Measuring the shape of a sample is done a little differently than measuring the shape of a population, however. The reason behind the difference is the desire to have the sample measurement serve as an unbiased estimator of the population measurement. If we took all of the possible samples of a certain size, n, from a population and found the variance of each one, and then found the mean of those sample variances, that mean would be a little smaller than the variance of the population.
You can see why this is so if you think it through. If you knew the population mean, you could find 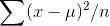 for each sample, and have an unbiased estimate for
for each sample, and have an unbiased estimate for 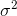 . However, you do not know the population mean, so you will have to infer it. The best way to infer the population mean is to use
the sample mean
. However, you do not know the population mean, so you will have to infer it. The best way to infer the population mean is to use
the sample mean 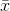 . The variance of a sample will then be found by
averaging together all of the
. The variance of a sample will then be found by
averaging together all of the 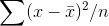 .
.
The mean of a sample is obviously determined by where the members of that sample lie. If you have a sample that is mostly from the high (or right) side of a population's distribution, then the
sample mean will almost for sure be greater than the population mean. For such a sample, 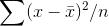 would underestimate
would underestimate 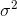 . The same is true for samples that are mostly from the low (or left) side of the population. If you think about what kind of
samples will have
. The same is true for samples that are mostly from the low (or left) side of the population. If you think about what kind of
samples will have 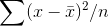 that is greater than the
population
that is greater than the
population 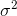 , you will come to the realization that it is only
those samples with a few very high members and a few very low members—and there are not very many samples like that. By now you should have convinced yourself that
, you will come to the realization that it is only
those samples with a few very high members and a few very low members—and there are not very many samples like that. By now you should have convinced yourself that 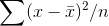 will result in a biased estimate of
will result in a biased estimate of 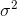 . You can see that, on average, it is too small.
. You can see that, on average, it is too small.
How can an unbiased estimate of the population variance, 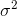 , be
found? If
, be
found? If 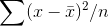 is on average too small, we need to do
something to make it a little bigger. We want to keep the
is on average too small, we need to do
something to make it a little bigger. We want to keep the 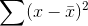 , but if we divide it by something a little smaller, the result will be a little larger. Statisticians have found out that the
following way to compute the sample variance results in an unbiased estimator of the population variance:
, but if we divide it by something a little smaller, the result will be a little larger. Statisticians have found out that the
following way to compute the sample variance results in an unbiased estimator of the population variance:
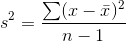
If we took all of the possible samples of some size, n, from a population, and found the sample variance for each of those samples, using this formula, the mean of those sample variances would
equal the population variance, 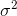 .
.
Note that we use s2 instead of 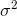 , and n instead of
N (really "nu", not "en") since this is for a sample and we want to use the Roman letters rather than the Greek letters, which are used for populations.
, and n instead of
N (really "nu", not "en") since this is for a sample and we want to use the Roman letters rather than the Greek letters, which are used for populations.
There is another way to see why you divide by n-1. We also have to address something called "degrees of freedom" before too long, and it is the degrees of freedom that is the key of the other explanation. As we go through this explanation, you should be able to see that the two explanations are related.
Imagine that you have a sample with 10 members (n=10), and you want to use it to estimate the variance of the population form which it was drawn. You write each of the 10 values on a separate
scrap of paper. If you know the population mean, you could start by computing all 10 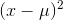 . In the usual case, you do not know
. In the usual case, you do not know 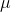 , however, and you must start by finding
, however, and you must start by finding 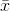 from the values on the 10 scraps to use as an estimate of m. Once you have found
from the values on the 10 scraps to use as an estimate of m. Once you have found 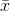 , you could lose any one of the 10 scraps and still be able to find the value that was on
the lost scrap form and the other 9 scraps. If you are going to use
, you could lose any one of the 10 scraps and still be able to find the value that was on
the lost scrap form and the other 9 scraps. If you are going to use 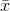 in the formula for sample variance, only 9 (or n-1), of the x's are free to take on any value. Because only n-1 of the x's can
vary freely, you should divide
in the formula for sample variance, only 9 (or n-1), of the x's are free to take on any value. Because only n-1 of the x's can
vary freely, you should divide 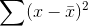 by n-1, the number
of (x’s) that are really free. Once you use
by n-1, the number
of (x’s) that are really free. Once you use 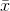 in the formula for
sample variance, you use up one "degree of freedom", leaving only n-1. Generally, whenever you use something you have previously computed from a sample within a formula, you use up a degree of
freedom.
in the formula for
sample variance, you use up one "degree of freedom", leaving only n-1. Generally, whenever you use something you have previously computed from a sample within a formula, you use up a degree of
freedom.
A little thought will link the two explanations. The first explanation is based on the idea that 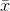 , the estimator of
, the estimator of 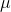 , varies with the sample. It is because
, varies with the sample. It is because 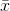 varies with the sample that a degree of freedom is used up in the second explanation.
varies with the sample that a degree of freedom is used up in the second explanation.
The sample standard deviation is found simply by taking the square root of the sample variance:
![s=\sqrt{[\sum (x-\bar{x})^{2}/(n-1)]}](/system/files/resource/31/31475/31581/media/eqn-img_28.gif)
While the sample variance is an unbiased estimator of population variance, the sample standard deviation is not an unbiased estimator of the population standard deviation—the square root of the
average is not the same as the average of the square roots. This causes statisticians to use variance where it seems as though they are trying to get at standard deviation. In general,
statisticians tend to use variance more than standard deviation. Be careful with formulas using sample variance and standard deviation in the following chapters. Make sure you are using the
right one. Also note that many calculators will find standard deviation using both the population and sample formulas. Some use 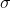 and s to show the difference between population and sample formulas, some use sn and sn-1 to show the
difference.
and s to show the difference between population and sample formulas, some use sn and sn-1 to show the
difference.
If Ann Howard wanted to infer what the population distribution of volleyball players' sock sizes looked like she could do so from her sample. If she is going to send volleyball coaches packages of socks for the players to try, she will want to have the packages contain an assortment of sizes that will allow each player to have a pair that fits. Ann wants to infer what the distribution of volleyball players sock sizes looks like. She wants to know the mean and variance of that distribution. Her data, again, is:
|
size |
frequency |
|
6 |
3 |
|
7 |
24 |
|
8 |
33 |
|
9 |
20 |
|
10 |
17 |
The mean sock size can be found:
=[(3x6)+(24x7)+(33x8)+(20x9)+(17x10)]/97 = 8.25.
To find the sample standard deviation, Ann decides to use Excel. She lists the sock sizes that were in the sample in column B, and the frequency of each of those sizes in column C. For column
D, she has the computer find for each of 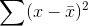 the sock
sizes, using the formula =(B1-8.25)^2 in the first row, and then copying it down to the other four rows. In E1, she multiplies D1, by the frequency using the formula =C1*D1, and copying it down
into the other rows. Finally, she finds the sample standard deviation by adding up the five numbers in column E and dividing by n-1 = 96 using the Excel formula =sum(E1:E5)/96. The spreadsheet
appears like this when she is done:
the sock
sizes, using the formula =(B1-8.25)^2 in the first row, and then copying it down to the other four rows. In E1, she multiplies D1, by the frequency using the formula =C1*D1, and copying it down
into the other rows. Finally, she finds the sample standard deviation by adding up the five numbers in column E and dividing by n-1 = 96 using the Excel formula =sum(E1:E5)/96. The spreadsheet
appears like this when she is done:
|
A |
B |
C |
D |
E |
|
1 |
6 |
3 |
5.06 |
15.19 |
|
2 |
7 |
24 |
1.56 |
37.5 |
|
3 |
8 |
33 |
0.06 |
2.06 |
|
4 |
9 |
20 |
0.56 |
11.25 |
|
5 |
10 |
17 |
3.06 |
52.06 |
|
6 |
n= |
97 |
Var = 1.217139 |
|
|
7 |
Std.dev = 1.10324 |
|||
|
8 |
Ann now has an estimate of the variance of the sizes of socks worn by college volleyball players, 1.22. She has inferred that the population of college volleyball players' sock sizes has a mean of 8.25 and a variance of 1.22.
- 1836 reads






