Do these populations have the same location? The Mann-Whitney U test.

In the chapter “The t-test”, you learned how to test to see if two samples came from populations with the same mean by using the t-test. If your samples are small and you are not sure if the original populations are normal, or if your data does not measure intervals, you cannot use that t-test because the sample t-scores will not follow the sampling distribution in the t-table. Though there are two different data problems that keep you from using the t-test, the solution to both problems is the same, the non-parametric Mann-Whitney U test. The basic idea behind the test is to put the samples together, rank the members of the combined sample, and then see if the two samples are mixed together in the common ranking.

Once you have a single ranked list containing the members of both samples, you are ready to conduct a Mann-Whitney U test. This test is based on a simple idea. If the first part of the combined ranking is largely made up of members from one sample, and the last part is largely made up of members from the other sample, then the two samples are probably from populations with different ”averages” and therefore different locations. You can test to see if the members of one sample are lumped together or spread through the ranks by adding up the ranks of each of the two groups and comparing the sums. If these "rank sums" are about equal, the two groups are mixed together. If these ranks sums are far from equal, each of the samples is lumped together at the beginning or the end of the overall ranking.

Willy Senn works for Old North Gadgets, a maker and marketer of computer peripherals aimed at scientists, consultants, and college faculty. Old North's home office and production facilities are in a small town in the US state of Maine. While this is a nice place to work, the firm wants to expand its sales and needs a sales office in a location closer to potential customers and closer to a major airport. Willy has been given the task of deciding where that office should be. Before he starts to look at office buildings and airline schedules, he needs to decide if Old North's potential customers are in the east or the west. Willy finds an article in Fortune magazine that lists the best cities for finding "knowledge workers", Old North's customers. That article lists the ten best cities in the United States.

Six of the top ten are in the east and four are in the west, but these ten represent only a sample of the market. It looks like the eastern places tend to be higher in the top ten, but is that really the case? If you add up the ranks, the six eastern cities have a "rank sum" of 31 while the western cities have a rank sum of 24, but there are more eastern cities and even if there were the same number would that difference be due to a different "average" in the rankings, or is it just due to sampling? The Mann-Whitney U test can tell you if the rank sum of 31 for the eastern cities is significantly less than would be expected if the two groups really were about the same and six of the ten in the sample happened to be from one group. The general formula for computing the Mann-Whitney U for the first of two groups is:

where:

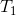 = the sum of the ranks of group 1
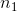 = the number of members of the sample from group 1
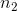= the number of members of the sample from group 2.

This formula seems strange at first, but a little careful thought will show you what is going on. The last third of the formula, -T₁, subtracts the rank sum of the group from the rest of the formula. What is the first two-thirds of the formula? The bigger the total of your two samples, and the more of that total that is in the first group, the bigger you would expect T₁ to be, everything else equal. Looking at the first two-thirds of the formula, you can see that the only variables in it are n₁ and n₂, the sizes of the two samples. The first two-thirds of the formula depends on the how big the total group is and how it is divided between the two samples. If eithe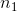r  or 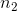 gets larger, so does this part of the formula. The first two-thirds of the formula is the maximum value for T₁, the rank sum of group 1. T₁ will be at its maximum if the members of the first group were all at the bottom of the rankings for the combined samples. The U₁ score then is the difference between the actual rank sum and the maximum possible. A bigger U₁ means that the members of group 1 are bunched more at the top of the rankings and a smaller U₁ means that the members of group 1 are bunched near the bottom of the rankings so that the rank sum is close to its maximum. Obviously, a U-score can be computed for either group, so there is always a U₁ and a U₂. If U₁ is larger, U₂ is smaller for a given n₁ and n₂ because if T₁ is smaller, T₂ is larger.

What should Willy expect if the best cities are in one region rather than being evenly distributed across the country? If the best cities are evenly distributed, then the eastern group and the western group should have U's that are close together since neither group will have a T that is close to either its minimum or its maximum. If the one group is mostly at the top of the list, then that group will have a large U since its T will be small, and the other group will have a smaller U since its T will be large. U₁ +  U₂ is always equal to n so either one can be used to test the hypothesis that the two groups come from the same population. Though there is always a pair of U-scores for any Mann-Whitney U-test, the published tables only show the smaller of the pair. Like all of the other tables you have used, this one shows what the sampling distribution of U's is like.

The sampling distribution, and this test, were first described by HB Mann and DR Whitney in 1947. 1 While you have to compute both U-scores, you only use the smaller one to test a two-tailed hypothesis. Because the tables only show the smaller U, you need to be careful when conducting a one-tail test. Because you will accept the alternative hypothesis if U is very small, you use the U computed for that sample which Ha: says is farther down the list. You are testing to see if one of the samples is located to the right of the other, so you test to see if the rank sum of that sample is large enough to make its U small enough to accept H_a :. If you learn to think through this formula, you will not have to memorize all of this detail because you will be able to figure out what to do.

Let us return to Willy 's problem. He needs to test to see if the best cities in which to locate the sales office, the best cities for finding "knowledge workers", are concentrated in one part of the country or not. He can attack his problem with a hypothesis test using the Mann-Whitney U-test. His hypotheses are:

H₀ : The distributions of eastern and western city rankings among the "best places to find knowledge workers" are the same.

H_a : The distributions are different.

Looking at the table of Mann-Whitney values, he finds the following if one of the n's is 6:

The values in the table show what portion of the sampling distribution of U-statistics is in the lower tail, below the U value in the first column, if the null hypothesis is true. Willy decides to use an 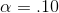. Since he will decide that the data supports H_a if either the east or the west has a small U, Willy has a two-tail test and needs to divide his a between the two tails. He will choose H_a if either U is in the lowest .05 of the distribution. Going down the column for the other n equal to 4, Willy finds that if the null hypothesis is true, the probability that the smaller of the two U-scores will be 4 or less is only .0571, and probability that the lower U-score will be 3 or less is .0333. His half 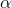of .05 is between these two, so he decides to be conservative and use as a decision rule to conclude that the data supports H_a: The distributions are different, if his sample U is less than 3 and that the data supports H₀: the distributions are the same, if his U is greater than or equal to 3. Now he computes his U, finding both U_e and U_w.

Remembering the formula from above, he finds his two U values::

For the eastern cities:

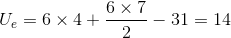
For the western cities:

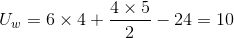
The smaller of his two U-scores is U_w = 10.Because 10 is larger than 3, his decision rule tells him that the data supports the null hypothesis that eastern and western cities rank about the same. Willy decides that the sales office can be in either an eastern or western city, at least based on locating the office close to near large numbers of knowledge workers. The decision will depend on office cost and availability and airline schedules.