Though the sample mean is an unbiased estimator of the population mean, very few samples have a mean exactly equal to the population mean. Though few samples have a mean, exactly equal to the
population mean, m, the central limit theorem tells us that most samples have a mean that is close to the population mean. As a result, if you use the central limit theorem to estimate
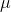, you will seldom be exactly right, but you will seldom be far
wrong. Statisticians have learned how often a point estimate will be how wrong. Using this knowledge you can find an interval, a range of values, which probably contains the population mean.
You even get to choose how great a probability you want to have, though to raise the probability, the interval must be wider.
Most of the time, estimates are interval estimates. When you make an interval estimate, you can say "I am z per cent sure that the mean of this population is between x and y". Quite often, you will hear someone say that they have estimated that the mean is some number "± so much". What they have done is quoted the midpoint of the interval for the "some number", so that the interval between x and y can then be split in half with + "so much" above the midpoint and -"so much" below. They usually do not tell you that they are only "z per cent sure". Making such an estimate is not hard— it is what Kevin Schmidt did at the end of the last chapter. It is worth your while to go through the steps carefully now, because the same basic steps are followed for making any interval estimate.
In making any interval estimate, you need to use a sampling distribution. In making an interval estimate of the population mean, the sampling distribution you use is the t-distribution.
The basic method is to pick a sample and then find the range of population means that would put your sample's t-score in the central part of the t-distribution. To make this a little clearer, look at the formula for t:
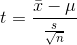
n is your sample's size and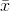 
and s are computed from your sample.
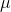is what you are trying to estimate. From the t-table, you can find
the range of t-scores that include the middle 80 per cent, or 90 per cent, or whatever per cent, for n-1 degrees of freedom. Choose the percentage you want and use the table. You now have the
lowest and highest t-scores,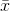 
, s and n. You can then substitute
the lowest t-score into the equation and solve for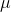 
to find one of
the limits for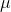 
if your sample's t-score is in the middle of the
distribution. Then substitute the highest t-score into the equation, and find the other limit. Remember that you want two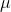 
's because you want to be able to say that the population mean is between two numbers.
The two t-scores are almost always ± the same number. The only heroic thing you have done is to assume that your sample has a t-score that is "in the middle" of the distribution. As long as your sample meets that assumption, the population mean will be within the limits of your interval. The probability part of your interval estimate, "I am z per cent sure that the mean is between...", or "with z confidence, the mean is between...", comes from how much of the t-distribution you want to include as "in the middle". If you have a sample of 25 (so there are 24df), looking at the table you will see that .95 of all samples of 25 will have a t-score between ±2.064; that also means that for any sample of 25, the probability that its t is between ±2.064 is .95.
As the probability goes up, the range of t-scores necessary to cover the larger proportion of the sample gets larger. This makes sense. If you want to improve the chance that your interval contains the population mean, you could simply choose a wider interval. For example, if your sample mean was 15, sample standard deviation was 10, and sample size was 25, to be .95 sure you were correct, you would need to base your mean on t-scores of ±2.064. Working through the arithmetic gives you an interval from 10.872 to 19.128. To have .99 confidence, you would need to base your interval on t-scores of ±2.797. Using these larger t-scores gives you a wider interval, one from 9.416 to 20.584. This trade-off between precision (a narrower interval is more precise) and confidence (probability of being correct), occurs in any interval estimation situation. There is also a trade-off with sample size. Looking at the t-table, note that the t-scores for any level of confidence are smaller when there are more degrees of freedom. Because sample size determines degrees of freedom, you can make an interval estimate for any level of confidence more precise if you have a larger sample. Larger samples are more expensive to collect, however, and one of the main reasons we want to learn statistics is to save money. There is a three-way trade-off in interval estimation between precision, confidence, and cost.
At Foothill Hosiery, John McGrath has become concerned that the hiring practices discriminate against older workers. He asks Kevin to look into the age at which new workers are hired, and Kevin
decides to find the average age at hiring. He goes to the personnel office, and finds out that over 2,500 different people have worked at Foothill in the past fifteen years. In order to save
time and money, Kevin decides to make an interval estimate of the mean age at date of hire. He decides that he wants to make this estimate with .95 confidence. Going into the personnel files,
Kevin chooses 30 folders, and records the birth date and date of hiring from each. He finds the age at hiring for each person, and computes the sample mean and standard deviation, finding
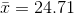years and s = 2.13 years. Going to the t-table, he finds
that .95 of t-scores with 29 df are between ±2.045. He solves two equations:
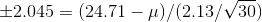and finds that the limits to his interval are
23.91 and 25.51. Kevin tells Mr. McGrath: "With .95 confidence, the mean age at date of hire is between 23.91 years and 25.51 years."
- 937 reads
