Another t-test: do these two (independent) samples come from populations with the same mean?

Available under Creative Commons-ShareAlike 4.0 International License.

One of the other statistics that has a sampling distribution that follows the t-distribution is the difference between two sample means. If samples of one size (n₁) are taken from one normal population and samples of another size (n₂) are taken from another normal population (and the populations have the same standard deviation), then a statistic based on the difference between the sample means and the difference between the population means is distributed like t with n₁ + n₂ −2 degrees of freedom. These samples are independent because the members in one sample do not affect which members are in the other sample. You can choose the samples independently of each other, and the two samples do not need to be the same size. The t-statistic is:

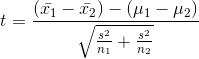
where: 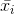= the mean of sample i
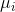             = the mean of population i
              s² = the pooled variance
              n_i = the size of sample i.

The usual case is to test to see if the samples come from populations with the same mean, the case where 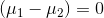. The pooled variance is simply a weighted average of the two sample variances, with the weights based on the sample sizes. This means that you will have to calculate the pooled variance before you calculate the t-score. The formula for pooled variance is:

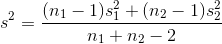
To use the pooled variance t-score, it is necessary to assume that the two populations have equal variances. If you are wondering about why statisticians make a strong assumption in order to use such a complicated formula, it is because the formula that does not need the assumption of equal variances is even more complicated, and reduces the degrees of freedom in the final statistic. In any case, unless you have small samples, the amount of arithmetic needed means that you will probably want to use a statistical software package for this test. You should also note that you can test to see if two samples come from populations that are any hypothesized distance apart by setting 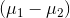equal to that distance.

An article in U. S. News and World Report (Nov. 1993) lamenting grade inflation in colleges states that economics grades have not been inflated as much as most other grades. Nora Alston chairs the Economics Department at Oaks College, and the dean has sent her a copy of the article with a note attached saying "Is this true here at Oaks? Let me know." Dr Alston is not sure if the Dean would be happier if economics grades were higher or lower than other grades, but the article claims that economics grades are lower. Her first stop is the Registrar's office.

She has the clerk in that office pick a sample of 10 class grade reports from across the college spread over the past three semesters.She also has the clerk pick out a sample of 10 reports for economics classes. She ends up with a total of 38 grades for economics classes and 51 grades for other classes. Her hypotheses are:

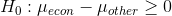
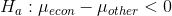
She decides to use .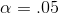

This is a lot of data, and Dr Alston knows she will want to use the computer to help. She initially thought she would use a spreadsheet to find the sample means and variances, but after thinking a minute, she decided to use a statistical software package. The one she is most familiar with is one called SAS. She loads SAS onto her computer, enters the data, and gives the proper SAS commands. The computer gives her the output in Table 5.2 SAS system software output for Dr Alston's grade study.

Dr Alston has 87 df, and has decided to use a one-tailed, left tail test with 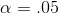. She goes to her t-table and finds that 87 df does not appear, the table skipping from 60 to 120 df. There are two things she could do. She could try to interpolate the t-score that leaves .05 in the tail with 87 df, or she could choose between the t-value for 60 and 120 in a conservative manner. Using the conservative choice is the best initial approach, and looking at her table she sees that for 60 df .05 of t-scores are less than -1.671,and for 120 df, .05 are less than -1.658. She does not want to conclude that the data supports economics grades being lower unless her sample t-score is far from zero, so she decides that she will accept H_a : if her sample t is to the left of -1.671. If her sample t happens to be between -1.658 and -1.671, she will have to interpolate.

Looking at the SAS output, Dr Alston sees that her t-score for the equal variances formula is -2.3858, which is well below -1.671. She concludes that she will tell the dean that economics grades are lower than grades elsewhere at Oaks College.

Notice that SAS also provides the t-score and df for the case where equal variances are not assumed in the "unequal" line. SAS also provides a P value, but it is for a two-tail test because it gives the probability that a t with a larger absolute value, >|T|, occurs. Be careful when using the p values from software: notice if they are one-tail or two-tail p-values before you make your report!