This seems wrong—we will test a hypothesis about means by "analyzing variance". It is not wrong, but rather a really clever insight that some statistician had years ago. This idea —looking at variance to find out about differences in means—is the basis for much of the multivariate statistics used by researchers today. The ideas behind ANOVA are used when we look for relationships between two or more variables, the big reason we use multivariate statistics.
Testing to see if three or more samples come from populations with the same mean can often be a sort of multivariate exercise. If the three samples came from three different factories or were subject to different treatments, we are effectively seeing if there is a difference in the results because of different factories or treatments —is there a relationship between factory (or treatment) and the outcome?
Think about three samples. A group of x's have been collected, and for some good reason (other than their x value) they can be divided into three groups. You have some x's from group (sample) 1, some from group (sample) 2, and some from group (sample) 3. If the samples were combined, you could compute a "grand mean" and a "total variance" around that grand mean. You could also find the mean and (sample) "variance within" each of the groups. Finally, you could take the three sample means, and find the "variance between" them. ANOVA is based on analyzing where the "total" variance comes from. If you picked one x, the source of its variance, its distance from the grand mean would have two parts: (1) how far it is from the mean of its sample, and (2) how far its sample's mean is from the grand mean. If the three samples really do come from populations with different means, then for most of the x's, the distance between the sample mean and the grand mean will probably be greater than the distance between the x and its group mean. When these distances are gathered together and turned into variances, you can see that if the population means are different, the variance between the sample means is likely to be greater than the variance within the samples.
By this point in the book, it should not surprise you to learn that statisticians have found that if three or more samples are taken from a normal population, and the variance between the samples is divided by the variance within the samples, a sampling distribution formed by doing that over and over will have a known shape. In this case it will be distributed like F with m-1, n-m df, where m is the number of samples and n is the size of the m samples altogether. "Variance between" is found by:

where xj is the mean of sample j, and x is the "grand mean".
The numerator of the variance between is the sum of the squares of the distance between each x's sample mean and the grand mean. It is simply a summing of one of those sources of variance across all of the observations.
The "variance within" is found by:
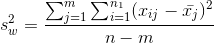
Double sums need to be handled with care. First (operating on the "inside" or second sum sign) find the mean of each sample and the sum of the squares of the distances of each x in the sample from its mean. Second (operating on the "outside" sum sign), add together the results from each of the samples.
The strategy for conducting a one-way analysis of variance is simple. Gather m samples. Compute the variance between the samples, the variance within the samples, and the ratio of between to within, yielding the F-score. If the F-score is less than one, or not much greater than one, the variance between the samples is no greater than the variance within the samples and the samples probably come from populations with the same mean. If the F-score is much greater than one, the variance between is probably the source of most of the variance in the total sample, and the samples probably come from populations with different means.
The details of conducting a one-way ANOVA fall into three categories: (1) writing hypotheses, (2) keeping the calculations organized, and (3) using the F-tables. The null hypothesis is that all of the population means are equal, and the alternative is that not all of the means are equal. Quite often, though two hypotheses are really needed for completeness, only H0 : is written:
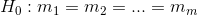
Keeping the calculations organized is important when you are finding the variance within. Remember that the variance within is found by squaring, and then summing, the distance between each observation and the mean of its sample. Though different people do the calculations differently, I find the best way to keep it all straight is to find the sample means, find the squared distances in each of the samples, and then add those together. It is also important to keep the calculations organized in the final computing of the F-score. If you remember that the goal is to see if the variance between is large, then its easy to remember to divide variance between by variance within.
Using the F-tables is the second detail. Remember that F-tables are one-tail tables and that ANOVA is a one-tail test. Though the null hypothesis is that all of the means are equal, you are testing that hypothesis by seeing if the variance between is less than or equal to the variance within. The number of degrees of freedom is m-1, n-m, where m is the number of samples and n is the total size of all the samples together.
- 3037 reads






