If this was a statistics course for math majors, you would probably have to prove this theorem. Because this text is designed for business and other non-math students, you will only have to learn to understand what the theorem says and why it is important. To understand what it says, it helps to understand why it works. Here is an explanation of why it works.
The theorem is about sampling distributions and the relationship between the location and shape of a population and the location and shape of a sampling distribution generated from that population. Specifically, the central limit theorem explains the relationship between a population and the distribution of sample means found by taking all of the possible samples of a certain size from the original population, finding the mean of each sample, and arranging them into a distribution.
The sampling distribution of means is an easy concept. Assume that you have a population of x's. You take a sample of n of those x's and find the mean of that sample, giving you one 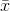 . Then take another sample of the same size, n, and find its
. Then take another sample of the same size, n, and find its 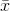 ...Do this over and over until you have chosen all possible samples of
size n. You will have generated a new population, a population of
...Do this over and over until you have chosen all possible samples of
size n. You will have generated a new population, a population of 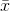 's. Arrange this population into a distribution, and you have the sampling distribution of means. You could find the sampling
distribution of medians, or variances, or some other sample statistic by collecting all of the possible samples of some size, n, finding the median, variance, or other statistic about each
sample, and arranging them into a distribution.
's. Arrange this population into a distribution, and you have the sampling distribution of means. You could find the sampling
distribution of medians, or variances, or some other sample statistic by collecting all of the possible samples of some size, n, finding the median, variance, or other statistic about each
sample, and arranging them into a distribution.
The central limit theorem is about the sampling distribution of means. It links the sampling distribution of 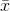 ’s with the original distribution of x's. It tells us that:
’s with the original distribution of x's. It tells us that:
(1) The mean of the sample means equals the mean of the original population, 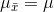 . This is what makes
. This is what makes 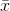 an unbiased estimator of
an unbiased estimator of 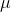 .
.
(2) The distribution of 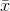 ’s will be bell-shaped, no
matter what the shape of the original distribution of x's.
’s will be bell-shaped, no
matter what the shape of the original distribution of x's.
This makes sense when you stop and think about it. It means that only a small portion of the samples have means that are far from the population mean. For a
sample to have a mean that is far from 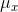 , almost all of its
members have to be from the right tail of the distribution of x's, or almost all have to be from the left tail. There are many more samples with most of their members from the middle of the
distribution, or with some members from the right tail and some from the left tail, and all of those samples will have an
, almost all of its
members have to be from the right tail of the distribution of x's, or almost all have to be from the left tail. There are many more samples with most of their members from the middle of the
distribution, or with some members from the right tail and some from the left tail, and all of those samples will have an 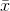 close to
close to 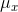 .
.
(3a) The larger the samples, the closer the sampling distribution will be to normal, and
(3b) if the distribution of x's is normal, so is the distribution of 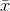 ’s.
’s.
These come from the same basic reasoning as (2), but would require a formal proof since "normal distribution" is a mathematical concept. It is not too hard
to see that larger samples will generate a "more-bell-shaped" distribution of sample means than smaller samples, and that is what makes (3a) work.
(4) The variance of the 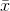 ’s is equal to the variance of the x's
divided by the sample size, or:
’s is equal to the variance of the x's
divided by the sample size, or:
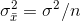
therefore the standard deviation of the sampling distribution is:
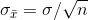
While it is difficult to see why this exact formula holds without going through a formal proof, the basic idea that larger samples yield sampling distributions with smaller standard deviations
can be understood intuitively. If 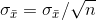 then
then 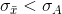 . Furthermore, when the sample size, n, rises,
. Furthermore, when the sample size, n, rises, 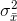 gets smaller. This is because it becomes more unusual to get a sample with an
gets smaller. This is because it becomes more unusual to get a sample with an 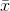 that is far from
that is far from 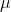 as n gets larger. The standard deviation of the sampling distribution includes an
as n gets larger. The standard deviation of the sampling distribution includes an 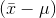 for each, but remember that there are not many
for each, but remember that there are not many 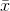 's that are as far from
's that are as far from 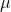 as there are x's that are far from
as there are x's that are far from 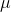 , and as n grows there are fewer and fewer samples with an
, and as n grows there are fewer and fewer samples with an 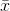 far from
far from 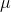 . This means that there are not many
. This means that there are not many 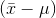 that are as large as quite a few
that are as large as quite a few 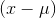 are. By the time you square everything, the average
are. By the time you square everything, the average 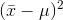 is going to be much smaller than the average
is going to be much smaller than the average 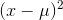 , so,
, so, 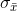 is going to be smaller than
is going to be smaller than 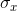 . If the mean volume of soft drink in a population of 12 ounce cans is 12.05 ounces with a variance of .04 (and a standard
deviation of .2), then the sampling distribution of means of samples of 9 cans will have a mean of 12.05 ounces and a variance of .04/9=.0044 (and a standard deviation of .2/3=.0667).
. If the mean volume of soft drink in a population of 12 ounce cans is 12.05 ounces with a variance of .04 (and a standard
deviation of .2), then the sampling distribution of means of samples of 9 cans will have a mean of 12.05 ounces and a variance of .04/9=.0044 (and a standard deviation of .2/3=.0667).
You can follow this same line of reasoning once again, and see that as the sample size gets larger, the variance and standard deviation of the sampling distribution will get smaller. Just
remember that as sample size grows, samples with an 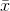 that is far
from
that is far
from 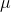 get rarer and rarer, so that the average
get rarer and rarer, so that the average 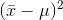 will get smaller. The average
will get smaller. The average 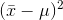 is the variance. If larger samples of soft drink bottles are taken, say samples of
16, even fewer of the samples will have means that are very far from the mean of 12.05 ounces. The variance of the sampling distribution when n=16 will therefore be smaller. According to what
you have just learned, the variance will be only .04/16=.0025 (and the standard deviation will be .2/4=.05). The formula matches what logically is happening; as the samples get bigger, the
probability of getting a sample with a mean that is far away from the population mean gets smaller, so the sampling distribution of means gets narrower and the variance (and standard deviation)
get smaller. In the formula, you divide the population variance by the sample size to get the sampling distribution variance. Since bigger samples means dividing by a bigger number, the
variance falls as sample size rises. If you are using the sample mean as to infer the population mean, using a bigger sample will increase the probability that your inference is very close to
correct because more of the sample means are very close to the population mean. There is obviously a trade-off here. The reason you wanted to use statistics in the first place was to avoid
having to go to the bother and expense of collecting lots of data, but if you collect more data, your statistics will probably be more accurate.
is the variance. If larger samples of soft drink bottles are taken, say samples of
16, even fewer of the samples will have means that are very far from the mean of 12.05 ounces. The variance of the sampling distribution when n=16 will therefore be smaller. According to what
you have just learned, the variance will be only .04/16=.0025 (and the standard deviation will be .2/4=.05). The formula matches what logically is happening; as the samples get bigger, the
probability of getting a sample with a mean that is far away from the population mean gets smaller, so the sampling distribution of means gets narrower and the variance (and standard deviation)
get smaller. In the formula, you divide the population variance by the sample size to get the sampling distribution variance. Since bigger samples means dividing by a bigger number, the
variance falls as sample size rises. If you are using the sample mean as to infer the population mean, using a bigger sample will increase the probability that your inference is very close to
correct because more of the sample means are very close to the population mean. There is obviously a trade-off here. The reason you wanted to use statistics in the first place was to avoid
having to go to the bother and expense of collecting lots of data, but if you collect more data, your statistics will probably be more accurate.
- 2182 reads






