Power in the Frequency Domain

Available under Creative Commons-ShareAlike 4.0 International License.

Recalling that the instantaneous power consumed by a circuit element or an equivalent circuit that represents a collection of elements equals the voltage times the current entering the positive-voltage terminal, p (t)= v (t) i (t), what is the equivalent expression using impedances? The resulting calculation reveals more about power consumption in circuits and the introduction of the concept of average power.

When all sources produce sinusoids of frequency f, the voltage and current for any circuit element or collection of elements are sinusoids of the same frequency.

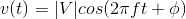
$v(t)=|V|cos(2\pi ft+\phi)$

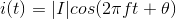
$i(t)=|I|cos(2\pi ft+\theta)$

Here, the complex amplitude of the voltage V equals |V |e^j^φ and that of the current is |I|e^j^θ. We can also write the voltage and current in terms of their complex amplitudes using Euler's formula (Euler's Formula).

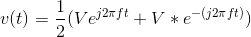
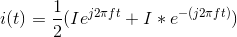
$i(t)=\frac{1}{2}(Ie^{j2\pi ft}+I*e^{-(j2\pi ft)})$

Multiplying these two expressions and simplifying gives

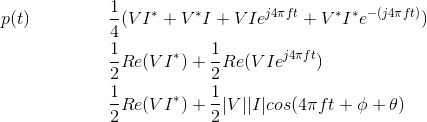
$\begin{align*} p(t)\ \ \ \ \ \ \ \ \ \ \ \ \ & \frac{1}{4}(VI^{*}+V^{*}I+VIe^{j4\pi ft}+V^{*}I^{*}e^{-(j4\pi ft)})\\ &\frac{1}{2}Re(VI^{*})+\frac{1}{2}Re(VIe^{j4\pi ft})\\ &\frac{1}{2}Re(VI^{*})+\frac{1}{2}|V||I|cos(4\pi ft+\phi+\theta)\\ \end{align*}$

We define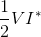 $\frac{1}{2}VI^{*}$ to be complex power. The real-part of complex power is the first term and since it does not change with time, it represents the power consistently consumed/produced by the circuit. The second term varies with time at a frequency twice that of the source. Conceptually, this term details how power "sloshes" back and forth in the circuit because of the sinusoidal source.

From another viewpoint, the real-part of complex power represents long-term energy consumption/production. Energy is the integral of power and, as the integration interval increases, the first term appreciates while the time-varying term "sloshes." Consequently, the most convenient Definition of the average power consumed/produced by any circuit is in terms of complex amplitudes.

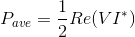
$P_{ave}=\frac{1}{2}Re(VI^{*})$

Exercise 3.11.1

Suppose the complex amplitudes of the voltage and current have fixed magnitudes. What phase relationship between voltage and current maximizes the average power? In other words, how are φ and θ related for maximum power dissipation?

Because the complex amplitudes of the voltage and current are related by the equivalent impedance, average power can also be written as
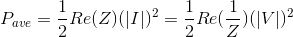
$P_{ave}=\frac{1}{2}Re(Z)(|I|)^2=\frac{1}{2}Re(\frac{1}{Z})(|V|)^2$

These expressions generalize the results (3.3) we obtained for resistor circuits. We have derived a fundamental result: Only the real part of impedance contributes to long-term power dissipation. Of the circuit elements, only the resistor dissipates power. Capacitors and inductors dissipate no power in the long term. It is important to realize that these statements apply only for sinusoidal sources. If you turn on a constant voltage source in an RC-circuit, charging the capacitor does consume power.

Exercise 3.11.2

In an earlier problem (Introduction Problems ), we found that the rms value of a sinusoid was 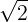$\sqrt{2}$ its amplitude divided by 2. What is average power expressed in terms of the rms values of the voltage and current (V_rms and I_rms respectively)?

5910 reads

You are here

Power in the Frequency Domain