Available under Creative Commons-ShareAlike 4.0 International License.
Systems that perform calculus-like operations on their inputs can produce waveforms signifcantly different than present in the input. Derivative systems operate in a straightforward way: A
first-derivative system would have the input-output relationship 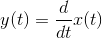 .
Integral systems have the complication that the integral's limits must be defined. It is a signal theory convention that the elementary integral operation have a lower limit of −∞, and that the
value of all signals at t = −∞ equals zero. A simple integrator would have input-output relation
.
Integral systems have the complication that the integral's limits must be defined. It is a signal theory convention that the elementary integral operation have a lower limit of −∞, and that the
value of all signals at t = −∞ equals zero. A simple integrator would have input-output relation
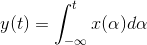
- 2173 reads






