Solution to Exercise 2.1.1
z + z* = a + jb + a − jb =2a =2Re (z). Similarly, z – z* = a + jb − (a − jb)=2jb = 2jIm (z)
Solution to Exercise 2.1.2
To convert 3 – 2j to polar form, we first locate the number in the complex plane in the fourth quadrant. The distance from the origin to the complex number is the magnitude r, which
equals 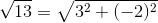 The angle equals
The angle equals 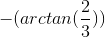 or −0.588 radians (−33.7 degrees). The final answer is
or −0.588 radians (−33.7 degrees). The final answer is 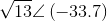 degrees.
degrees.
Solution to Exercise 2.1.3
zz* =(a + jb)(a − jb)= a2 + b2 . Thus, zz* = r2=(|z|)2 .
Solution to Exercise 2.3.1
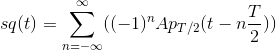
Solution to Exercise 2.6.1
In the first case, order does not matter; in the second it does. "Delay" means t → t − τ. "Time-reverse" means t →−t
Case 1 y (t)= Gx (t −τ), and the way we apply the gain and delay the signal gives the same result.
Case 2 Time-reverse then delay: y (t)= x (− (t −τ )) = x (−t + τ). Delay then time-reverse: y (t)= x ((−t) −τ ).
- 5337 reads






