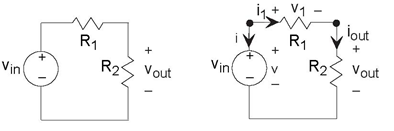
At every node, the sum of all currents entering or leaving a node must equal zero. What this law means physically is that charge cannot accumulate in a node; what goes in must come out. In the example, Figure 3.6, below we have a three-node circuit and thus have three KCL equations.

Note that the current entering a node is the negative of the current leaving the node.
Given any two of these KCL equations, we can find the other by adding or subtracting them. Thus, one of them is redundant and, in mathematical terms, we can discard any one of them. The convention is to discard the equation for the (unlabeled) node at the bottom of the circuit.
Exercise 3.4.1
In writing KCL equations, you will find that in an n-node circuit, exactly one of them is always redundant. Can you sketch a proof of why this might be true? Hint: It has to do with the fact that charge won't accumulate in one place on its own.
- 3143 reads






