To understand digital signal processing systems, we must understand a little about how computers compute. The modern definition of a computer is an electronic device that performs calculations on data, presenting the results to humans or other computers in a variety of (hopefully useful) ways.
Organization of a Simple Computer
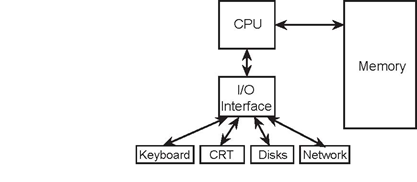
The generic computer contains input devices (keyboard, mouse, A/D (analog-to-digital) converter, etc.), a computational unit, and output devices (monitors, printers, D/A converters). The computational unit is the computer's heart, and usually consists of a central processing unit (CPU), a memory, and an input/output (I/O) interface. What I/O devices might be present on a given computer vary greatly.
- A simple computer operates fundamentally in discrete time. Computers are clocked devices, in which computational steps occur periodically according to ticks of a clock. This description be lies clock speed: When you say "I have a 1 GHz computer," you mean that your computer takes 1 nanosecond to perform each step. That is incredibly fast! A "step" does not, unfortunately, necessarily mean a computation like an addition; computers break such computations down into several stages, which means that the clock speed need not express the computational speed. Computational speed is expressed in units of millions of instructions/second (Mips). Your 1 GHz computer (clock speed) may have a computational speed of 200 Mips.
- Computers perform integer (discrete-valued) computations. Computer calculations can be numeric (obeying the laws of arithmetic), logical (obeying the laws of an algebra), or symbolic (obeying any law you like).4 Each computer instruction that performs an elementary numeric calculation an addition, a multiplication, or a division does so only for integers. The sum or product of two integers is also an integer, but the quotient of two integers is likely to not be an integer. How does a computer deal with numbers that have digits to the right of the decimal point? This problem is addressed by using the so-called floating-point representation of real numbers. At its heart, however, this representation relies on integer-valued computations.
- 2447 reads






