Complex Exponentials

Available under Creative Commons-ShareAlike 4.0 International License.

The most important signal is, of course, the complex exponential sequence.

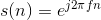
$s(n)=e^{j2\pi fn}$

Note that the frequency variable f is dimensionless and that adding an integer to the frequency of the discrete-time complex exponential has no effect on the signal's value.

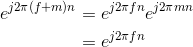
$\begin{align*} e^{j2\pi(f+m)n}&=e^{j2\pi fn }e^{j2\pi mn}\\ &=e^{j2\pi fn}\\ \end{align*}$

This derivation follows because the complex exponential evaluated at an integer multiple of 2π equals one. Thus, we need only consider frequency to have a value in some unit-length interval.

1164 reads

You are here

Complex Exponentials