The second-most important discrete-time signal is the unit sample, which is defined to be
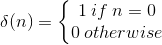
(5.14)

Examination of a discrete-time signal's plot, like that of the cosine signal shown in Figure 5.7(Cosine), reveals that all signals consist of a sequence of delayed and scaled unit samples. Because the value of a sequence at each integer m is denoted by s(m) and the unit sample delayed to occur at m is written δ(n - m), we can decompose any signal as a sum of unit samples delayed to the appropriate location and scaled by the signal value.
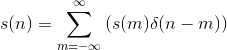
This kind of decomposition is unique to discrete-time signals, and will prove useful subsequently.
- 2725 reads






