We have mentioned that communications are, to varying degrees, subject to interference and noise. It's time to be more precise about what these quantities are and how they difer.
Interference represents man-made signals. Telephone lines are subject to power-line interference (in the United States a distorted 60 Hz sinusoid). Cellular telephone channels are subject to adjacent-cell phone conversations using the same signal frequency. The problem with such interference is that it occupies the same frequency band as the desired communication signal, and has a similar structure.
Exercise 6.8.1
Suppose interference occupied a different frequency band; how would the receiver remove it?
We use the notation i (t) to represent interference. Because interference has man-made structure, we can write an explicit expression for it that may contain some unknown aspects (how large it is, for example).
Noise signals have little structure and arise from both human and natural sources. Satellite channels are subject to deep space noise arising from electromagnetic radiation pervasive in the galaxy. Thermal noise plagues all electronic circuits that contain resistors. Thus, in receiving small amplitude signals, receiver amplifiers will most certainly add noise as they boost the signal's amplitude. All channels are subject to noise, and we need a way of describing such signals despite the fact we can't write a formula for the noise signal like we can for interference. The most widely used noise model is white noise. It is defined entirely by its frequency-domain characteristics.
- White noise has constant power at all frequencies.
- At each frequency, the phase of the noise spectrum is totally uncertain: It can be any value in between 0 and 2π, and its value at any frequency is unrelated to the phase at any other frequency.
- When noise signals arising from two different sources add, the resultant noise signal has a power equal to the sum of the component powers.
Because of the emphasis here on frequency-domain power, we are led to define the power spectrum. Because of Parseval's Theorem9, we define the power spectrum Ps (f) of a non-noise signal s (t) to be the magnitude-squared of its Fourier transform.
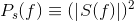
(6.21)
Integrating the power spectrum over any range of frequencies equals the power the signal contains in that band. Because signals must have negative frequency components that mirror positive frequency ones, we routinely calculate the power in a spectral band as the integral over positive frequencies multiplied by two.
![Power\: in\:[f_{1},f_{2}]=2\int_{f_{1}}^{f_{2}}P_{s}(f)df](/system/files/resource/9/9648/9776/media/eqn-img_1.gif)
(6.22)
Using the notation n (t) to represent a noise signal's waveform, we define noise in terms of its power spectrum. For white noise, the power spectrum equals the constant 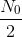 With this definition, the power in a frequency band equals N0
(f2 -f1).
With this definition, the power in a frequency band equals N0
(f2 -f1).
When we pass a signal through a linear, time-invariant system, the output's spectrum equals the product of the system's frequency response and the input's spectrum. Thus, the power spectrum of the system's output is given by
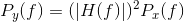
(6.23)
This result applies to noise signals as well. When we pass white noise through a filter, the output is also a noise signal but with power spectrum
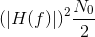
- 2571 reads






