Entropy

Available under Creative Commons-ShareAlike 4.0 International License.

Communication theory has been formulated best for symbolic-valued signals. Claude Shannon published in 1948 The Mathematical Theory of Communication, which became the cornerstone of digital communication. He showed the power of probabilistic models for symbolic-valued signals, which allowed him to quantify the information present in a signal. In the simplest signal model, each symbol can occur at index n with a probability Pr [a_k], k = {1,...,K} . What this model says is that for each signal value a K-sided coin is flipped (note that the coin need not be fair). For this model to make sense, the probabilities must be numbers between zero and one and must sum to one.

$0\leq Pr[a_{k}]\leq 1$

(6.48)

$\sum_{k=1}^{K}\left ( Pr[a_{k}] \right )=1$

(6.49)

This coin-flipping model assumes that symbols occur without regard to what preceding or succeeding symbols were, a false assumption for typed text. Despite this probabilistic model's over-simplicity, the ideas we develop here also work when more accurate, but still probabilistic, models are used. The key quantity that characterizes a symbolic-valued signal is the entropy of its alphabet.

$H(A)=-\left ( \sum_{k}\left ( Pr[a_{k}]\log_{2}\left ( Pr[a_{k}] \right ) \right ) \right )$

Because we use the base-2 logarithm, entropy has units of bits. For this Definition to make sense, we must take special note of symbols having probability zero of occurring. A zero-probability symbol never occurs; thus, we define 0log₂0=0 so that such symbols do not affect the entropy. The maximum value attainable by an alphabet's entropy occurs when the symbols are equally likely $\left ( Pr[a_{k}]=Pr[a_{l}] \right ).$ In this case, the entropy equals log₂ K. The minimum value occurs when only one symbol occurs; it has probability one of occurring and the rest have probability zero.

Exercise 6.20.1

Derive the maximum-entropy results, both the numeric aspect (entropy equals log₂K) and the theoretical one (equally likely symbols maximize entropy). Derive the value of the minimum entropy alphabet.

Example 6.1

A four-symbol alphabet has the following probabilities.

$Pr[a_{0}]=\frac{1}{2}$ $Pr[a_{1}]=\frac{1}{4}$ $Pr[a_{2}]=\frac{1}{8}$ $Pr[a_{3}]=\frac{1}{8}$

Note that these probabilities sum to one as they should. As 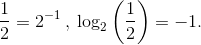$\frac{1}{2}=2^{-1}\:,\:\log_{2}\left ( \frac{1}{2} \right )=-1.$ The entropy of this alphabet equals

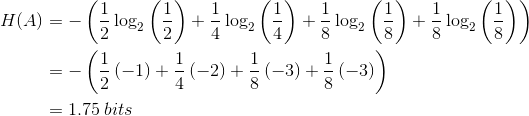
$\begin{align*}H(A)&=- \left (\frac{1}{2}\log_{2}\left ( \frac{1}{2} \right )+\frac{1}{4}\log_{2}\left ( \frac{1}{4} \right )+\frac{1}{8}\log_{2}\left ( \frac{1}{8} \right )+\frac{1}{8}\log_{2}\left ( \frac{1}{8} \right ) \right ) \\&=-\left (\frac{1}{2}\left ( -1 \right )+\frac{1}{4}\left ( -2 \right )+\frac{1}{8}\left ( -3 \right )+\frac{1}{8}\left ( -3 \right ) \right )\\&=1.75\:bits\end{align*}$

(6.51)

1569 reads

You are here

Entropy