Because of the higher datarate imposed by the channel coder, the probability of bit error occurring in the digital channel increases relative to the value obtained
when no channel coding is used. The bit interval duration must be reduced by 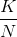 in comparison to the no-channel-coding situation, which means the energy per bit Eb goes down by the same amount. The bit interval must decrease by a factor of three if the transmitter is to keep up with the data stream, as illustrated here (Figure 6.21: Repetition Code).
in comparison to the no-channel-coding situation, which means the energy per bit Eb goes down by the same amount. The bit interval must decrease by a factor of three if the transmitter is to keep up with the data stream, as illustrated here (Figure 6.21: Repetition Code).
POINT OF INTEREST: It is unlikely that the transmitter's power could be increased to compensate.
Such is the sometimes-unfriendly nature of the real world.
Because of this reduction, the error probability pe of the digital channel goes up. The question thus becomes does channel coding really help: Is the effective error probability lower with channel coding even though the error probability for each transmitted bit is larger? The answer is no: Using a repetition code for channel coding cannot ultimately reduce the probability that a data bit is received in error. The ultimate reason is the repetition code's inefficiency: transmitting one data bit for every three transmitted is too inefficient for the amount of error correction provided.
Exercise 6.26.1
Using MATLAB, calculate the probability a bit is received incorrectly with a three-fold repetition code. Show that when the energy per bit Eb is reduced by 1/3 that this probability is larger than the no-coding probability of error.
Repetition Codes represents a special case of what is known as block
channel coding. For every K bits that enter the block channel coder, it inserts an additional N - K error-correction bits to produce a block of
N bits for transmission. We use the notation (N,K) to represent a given block code's parameters. In the three-fold Repetition Codes, K = 1 and N = 3. A block code's coding efficiency E equals the ratio 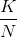 , and quantifies the overhead introduced by channel coding. The rate at which bits must be transmitted
again changes: So-called data bits b (n) emerge from the source coder at an average rate
, and quantifies the overhead introduced by channel coding. The rate at which bits must be transmitted
again changes: So-called data bits b (n) emerge from the source coder at an average rate 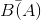 and exit the channel at a rate
and exit the channel at a rate 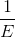 higher. We represent the fact that the bits sent through the digital channel operate at a different rate by using the index l
for the channel-coded bit stream c (l). Note that the blocking (framing) imposed by the channel coder does not correspond to symbol boundaries in the bit stream b (n),
especially when we employ variable-length source codes.
higher. We represent the fact that the bits sent through the digital channel operate at a different rate by using the index l
for the channel-coded bit stream c (l). Note that the blocking (framing) imposed by the channel coder does not correspond to symbol boundaries in the bit stream b (n),
especially when we employ variable-length source codes.
Does any error-correcting code reduce communication errors when real-world constraints are taken into account? The answer now is yes. To understand channel coding, we need to develop first a
general framework for channel coding, and discover what it takes for a code to be maximally efficient: Correct as many errors as possible using the fewest error correction bits as possible
(making the efficiency 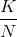 as large as possible).
as large as possible).
- 2422 reads






