Because the idea of channel coding has merit (so long as the code is efficient), let's develop a systematic procedure for performing channel decoding. One way of checking for errors is to try recreating the error correction bits from the data portion of the received block c. Using matrix notation, we make this calculation by multiplying the received block c by the matrix H known as the parity check matrix. It is formed from the generator matrix G by taking the bottom, error-correction portion of G and attaching to it an identity matrix. For our (7,4) code,
![H=\left [\underbrace{\begin{matrix} 1 & 1 & 1 & 0\\ 0 & 1 &1 &1 \\ 1 & 1 & 0 & 1 \end{matrix}}_{lower\:portion\:of\:G} \underbrace{\begin{matrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{matrix}}_{Identity} \right ]](/system/files/resource/9/9648/9796/media/eqn-img_1.gif)
(6.57)
The parity check matrix thus has size (N - K) × N, and the result of multiplying this matrix with a received word is a length- (N - K) binary vector. If no
digital channel errors occur we receive a codeword so that 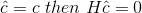 For example, the first column of G, (1, 0, 0, 0, 1, 0, 1)T , is a codeword. Simple calculations show that
multiplying this vector by H results in a length-(N - K) zero-valued vector.
For example, the first column of G, (1, 0, 0, 0, 1, 0, 1)T , is a codeword. Simple calculations show that
multiplying this vector by H results in a length-(N - K) zero-valued vector.
Exercise 6.28.1
Show that Hc =0 for all the columns of G. In other words, show that HG =0 an (N - K) × K matrix of zeroes. Does this property guarantee that all codewords also satisfy Hc=0?
When the received bits 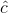 do not form a codeword,
do not form a codeword, 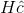 does not equal zero, indicating the presence of one or more errors induced by the digital channel. Because
the presence of an error can be mathematically written
as
does not equal zero, indicating the presence of one or more errors induced by the digital channel. Because
the presence of an error can be mathematically written
as
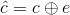
with e a vector of binary values having a 1 in those positions where a bit error occurred.
Exercise 6.28.2
Show that adding the error vector (1, 0,..., 0)T to a codeword fips the codeword's leading bit and leaves the rest unaffected.
Consequently,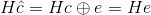 Because the result of the product is a
length-(N − K) vector of binary values, we can have 2N −
K − 1 non-zero values that correspond to non-zero error patterns e. To perform our channel decoding,
Because the result of the product is a
length-(N − K) vector of binary values, we can have 2N −
K − 1 non-zero values that correspond to non-zero error patterns e. To perform our channel decoding,
- compute (conceptually at least)
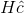
- if this result is zero, no detectable or correctable error occurred;
- if non-zero, consult a table of length-(N − K) binary vectors to associate them with the minimal error pattern that could have resulted in the non-zero result; then
- add the error vector thus obtained to the received vector
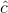 to correct the
error (because c ⊕ e ⊕ e =c).
to correct the
error (because c ⊕ e ⊕ e =c).
- Select the data bits from the corrected word to produce the received bit sequence
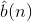
The phrase minimal in the third item raises the point that a double (or triple or quadruple ...) error occurring during the transmission/reception of one codeword can create the same received word as a single-bit error or no error in another codeword. For example, (1, 0, 0, 0, 1, 0, 1)Tand (0, 1, 0, 0, 1, 1, 1)T are both codewords in the example (7,4) code. The second results when the first one experiences three bit errors (first, second, and sixth bits). Such an error pattern cannot be detected by our coding strategy, but such multiple error patterns are very unlikely to occur. Our receiver uses the principle of maximum probability: An error-free transmission is much more likely than one with three errors if the bit-error probability pe is small enough.
Exercise 6.28.3
How small must pe be so that a single-bit error is more likely to occur than a triple-bit error?
- 2371 reads






