We implemented a hierarchy of Java classes for distributional models (Figure 3.3). Java is the standard programming language for Internet applications (Prodan & Prodan Mihai, 1997) ; this is the reason why we used this language to create the infrastructure for e-learning scenarios. We present below Java classes implemented for some distributions, as well as simulation examples.
Binomial distribution
package Distrib;
public class DistribBinomial extends DistributionDiscrete {
public DistribBinomial(int n, double p) { // Constructor
this.n = n;
this.p = p;
}
public double simValue() { // Simulation of a value
double U, rap, pp, F;
U = Math.random();
rap = p/(1-p);
pp = Math.exp(n*Math.log(1-p)); // probability X=i
F = pp; // F(i)=P{X<=i} distribution function
double k = 0;
while (U > F) {
pp = (rap*(n-k)/(k+1))*pp;
F = F + pp;
k++;
}
return k;
} // simValue()
public double initRecursion() {// Initial value for recursion
return Math.pow(1-p, n); // P{X=0}
}
public double valRecursion(int k) {// Value for recursion
return (double)(n-k)*p/(k+1)/(1-p);
}
int n;
double p;
} ///;
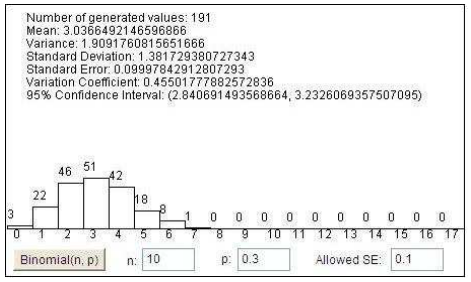
Poisson distribution
package Distrib;
public class DistribPoisson extends DistributionDiscrete {
public DistribPoisson(double lambda) { // Constructor
this.lambda = lambda;
}
public double simValue() { // Simulation of a value
double U, pp, F;
U = Math.random();
pp = Math.exp(-lambda); // probability X=i
F = pp; // F(i)=P{X<=i} distribution function
double k=0;
while (U > F) {
pp = lambda*pp/(k+1);
F = F + pp;
k++;
}
return k;
} // simValue()
public double initRecursion() { // Initial value for recursion
return Math.exp(-lambda); // P{X=0}
}
public double valRecursion(int k) { // Value for recursion
return (double)lambda/(k+1);
}
double lambda;
} ///;
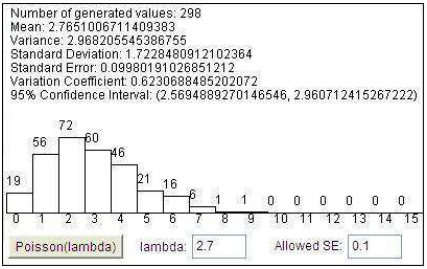
Geometric distribution
package Distrib;
public class DistribGeometric extends DistributionDiscrete {
public DistribGeometric(double p) { // Constructor
this.p = p;
}
public double simValue() { // Simulation of a value
double U; // geometric random variable in (0,1)
U = Math.random(); // Generate a random number
return (int)(Math.log(U)/Math.log(1-p));
} // simValue()
public double initRecursion() { // Initial value for recursion
return p; // P{X=0}
}
public double valRecursion(int k) { // Value for recursion
return 1-p;
}
double p;
} ///;
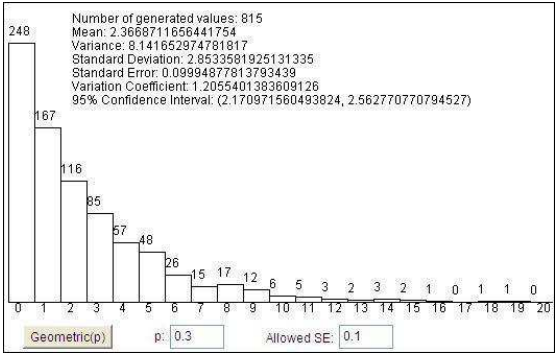
Uniform discrete distribution
package Distrib;
public class DistribDiscUniform extends DistributionDiscrete {
public DistribDiscUniform(int numb) { // Constructor
n = numb;
p = (double)1/n;
}
public double simValue() { // Simulation of a value
int X; // Random variable
double U; // Un iform random variable in (0,1)
U = Math.random(); // Generate a random number
return (int)(n*U);
} // simValue()
public double initRecursion() { // Initial value for recursion
return p; // P{X=0}
}
public double valRecursion(int k) { // Value for recursion
return (double) 1;
}
int n;
double p;
} ///;
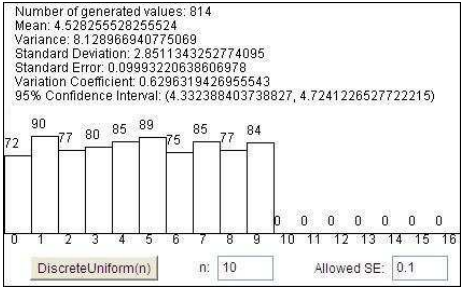
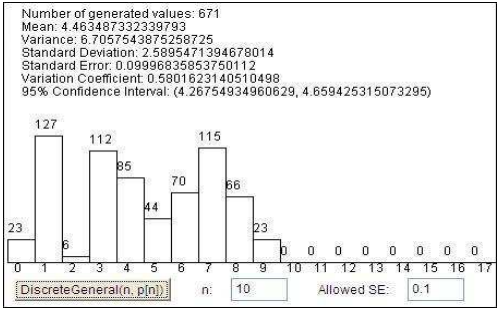
General discrete distribution
package Distrib;
public class DistribDiscGen extends DistributionDiscrete {
public DistribDiscGen(int n, double[] p) { // Constructor
this.n = n;
this.p = p;
for (int i=0; i<p.length; i++) {
if (pMax<p[i]) pMax=p[i];
}
c = pMax*n;
}
public double simValue() { // Simulation of a value
Distrib.DistribDiscUniform dDU = new DistribDiscUniform(n);
do {
Y = (int)dDU.simValue();
U = Math.random();
}
while (U > (double)(p[Y]/(c/n)));
return Y;
} // simValue()
int n, Y;
double pMax=0, c, U;
double[] p = new double[n];
} ///;
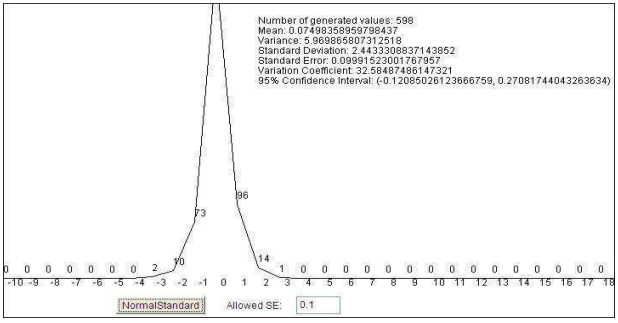
Normal standard distribution
package Distrib;
import Distrib.*;
import java.util.*;
public class DistribNormalS extends DistributionContinue {
public double simValue() { // Simulation of a value
double y1, y2, y, Z, U;
Distrib.DistribExponential Y1 = new Distrib.DistribExponential(1);
Distrib.DistribExponential Y2 = new Distrib.DistribExponential(1);
Random R = new Random();
do {
y1 = Y1.simValue();
y2 = Y2.simValue();
y = y2-Math.pow(y1-1, 2)/2;
} while (y<0);
U = R.nextDouble();
if (U<0.5) Z = y1;
else Z = -y1;
return Z;
} // simValue()
} ///;
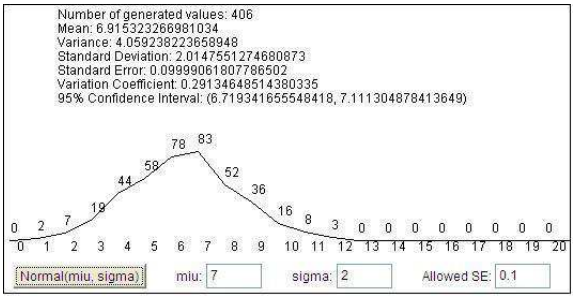
Normal distribution
package Distrib;
public class DistribNormal extends DistributionContinue {
public DistribNormal(double miu, double sigma) { // Constructor
this.miu = miu;
this.sigma = sigma;
}
public double simValue() { // Simulation of a value
double Z;
Z = NS.simValue();
X = miu+sigma*Z;
return X;
} // simValue()
double miu, sigma, X;
Distrib.DistribNormalS NS = new Distrib.DistribNormalS();
} ///;
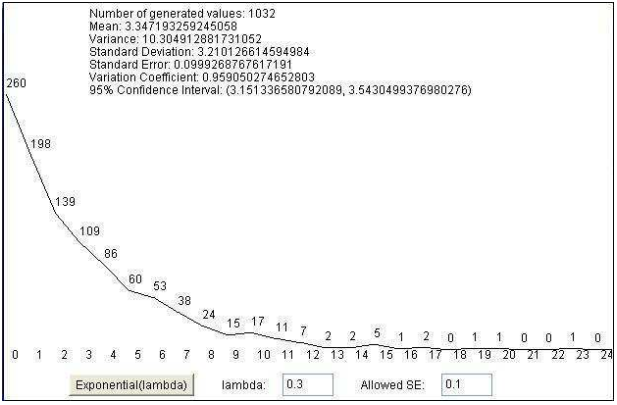
Exponential distribution
package Distrib;
public class DistribExponential extends DistributionContinue {
public DistribExponential(double lambda) { // Constructor
this.lambda = lambda;
}
public double simValue() { // Simulation of a value
U = Math.random();
X = -1/lambda*Math.log(U);
return X;
} // simValue()
double lambda, X, U;
} ///;
Gamma distribution
package Distrib;
public class DistribGamma extends DistributionContinue {
public DistribGamma(double lambda, int n) { // Constructor
this.lambda = lambda;
this.n = n;
}
public double simValue() { // Simulation of a value
double U, X=0;
for (int k=1; k<=n; k++) {
U = Math.random();
X = X-Math.log(U)/lambda;
}
return X;
} // simValue()
double lambda;
int n;
} ///;
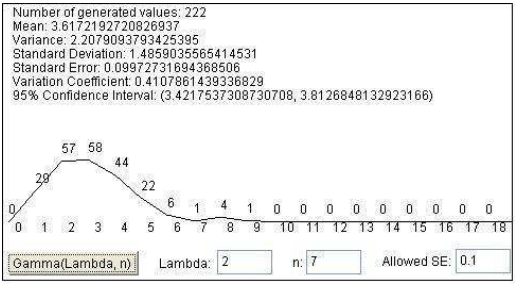
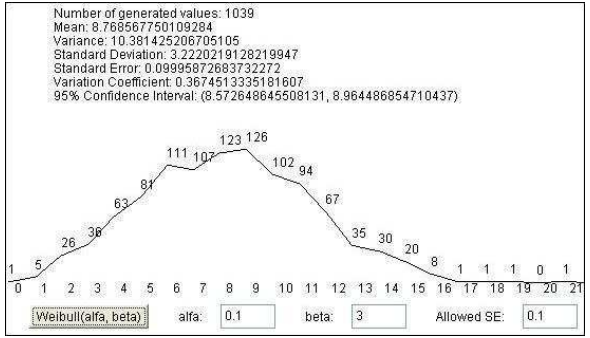
Weibull distribution
package Distrib;
public class DistribWeibull extends DistributionContinue {
public DistribWeibull(double alfa, double beta) { // Constructor
this.alfa = alfa;
this.beta = beta;
}
public double simValue() { // Simulation of a value
double U;
U = Math.random();
X = 1/alfa*Math.pow(-Math.log(U), 1/beta);
return X;
} // simValue()
double alfa, beta, X;
} ///;
- 2622 reads






