Mota (Mota, 2008) uses the neural networks to design two types of adaptability in an e-learning system: adaptive presentation and adaptive navigation. (http://paginas.fe.up.pt/~prodei/DSIE08/papers/35.pdf) The student model is defined considering Kolb learning styles inventory: Reflector, Theorist, Pragmatist and Activist student. The adaptation strategy uses SCORM 1.3 learning objects. The architecture proposed by Mota in (Mota, 2008) contains a Multilayer Perceptron trained with back propagation learning algorithm. The neural network is integrated in an intelligent unit, called CeLIP - Cesae eLearning Intelligent Player. Learners will have associated suitable learning objects according to their learning styles, user preferences and performance.
In (Seridi-Bouchelaghem, Sari, Sellami, 2005), there are used two neural networks: the former to select the appropriate basic units (“a basic unit is a multi-media document having intrinsically a teaching quality, i.e. which can be used within the framework of the knowledge transmission”) for the learner and the latter neural network is used when the learners do not pass the post-test and select base units having reinforcing roles.
An Artificial Neural Net model is used in (Seridi, H., Sari T., Sellami, M., 2006) in order to select in an adaptive way the learning basic unit. Viewing the problem of adaptive course generation upon learners’ profiles as a classification problem, the authors propose two neural networks:
The former neural network is used to select the adequate learning material in the first stage of learning and has the following properties:
- each neuron in the output layer is assigned to a learning material, referred as a basic unit in (Seridi, H., Sari T., Sellami, M., 2006);
- each neuron in the input layer represents the concepts related to the learning goal of the course;
- the hidden layer is used to computation and the number of neurons of the hidden layer is modified manually in the training stage.
The latter neural network is used in the reinforcement stage in the cases in which learners do not pass the test after the concepts training:
- The input of this network represents a grade of concepts’ understanding by the learners;
- The output layer is defined by the basic units having the reinforcing role.
The algorithm used for neural network’s training is backpropagation. The system proposed initially in the paper (Moise, 2010) and further extended in this chapter uses a conceptual map based representation of an electronic course, the ABC algorithm to initial assign Learning Units (containing different teaching models for the same concepts, theory etc.) and a neural network based intelligent engine to adjust the unfolding of the learning-teaching process to the learner’s needs.
An electronic course can be modelled using a conceptual map with k nodes (Figure 14.5) (Moise, Dumitrescu, 2003; Moise, Ionita, 2008)
Each node has associated more learning units (for a node i , we note the number of pedagogical resources with nLUi). The maxim number of combination is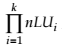 , so the teaching models are less than
, so the teaching models are less than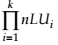 . A learning unit (LU) consists in pedagogical
resources and a teaching model. So, a node can be taught in different way using different learning units.
. A learning unit (LU) consists in pedagogical
resources and a teaching model. So, a node can be taught in different way using different learning units.
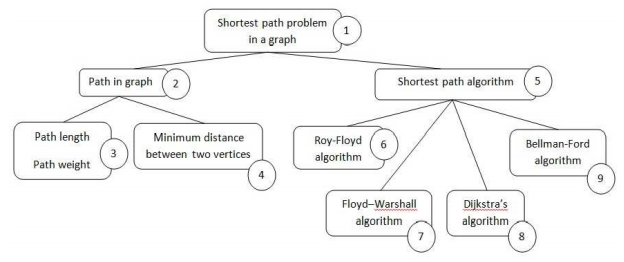
The problem of a right association between learners and learning units is solved in two phases:
1. Initial assignment between learners and LU using ABC algorithm;
2. Adaptation of the pedagogical path to each learner, by using neural network.
Phase 1
General Assignment Problem is represented by the necessity of assigning with a minimum cost a set of tasks to a set of agents with limited capacity. Each task can be assigned to single agents and uses certain of this agents’ resource.
These types of problems are common for the computer and communications area, vehicle routing, group technology, scheduling, etc.
This study aims to propose a solution for a General Assignment Problem using a Swarm Intelligence technique, represented by Artificial Bee Colony.
The proposed problem can be described as follows: a set of learners {L1,L2, . . . Ln} subscribe to attend a series of e-learning courses. In order to obtain information about the student’s experience, about his learning skills and his preferences, an e-questionnaire is completed at the moment of the platform registration. Taking into account this information a learners’ profile is associated to each candidate. On the e-learning platform there are a set of Learning Units for each e-course {LU1,LU2, . . . LUk}and the purpose is to assign each student to a proper Learning Unit in order to maximize students’ performance.
The bees will represent the Learning Units and the constraints associated regard the number of students that can simultaneously access a specific LU and the fact that one student can only access a single Learning Unit at the time.
The search space is represented by the learners. When a learner has assigned a Learning Unit, a fitness function is calculated considering the learners’ profile and the Learning Unit characteristics and the value of this fitness function needs to be maximized. Learners’ profile is defined using the instruction context (Moise, 2007):
- Mental context (MC) includes: general abilities and knowledge, the intelligence of the student, mental structure and the capacity of the learner to learn, understand and practice the material.
- Social context (SC) includes the familiar context, familiar stress, friends view.
- Technological context (TC) refers to course structure, format, informational technology, technological equipment.
- Knowledge context (KC) refers on previous knowledge, past experience related on the topic presented in course.
- Emotional context (EC) refers to the motivation, interest and goals of the students.
- Classroom context (CC) includes teaching methods, the structure of students (age, gender, ethnical structure, etc.)
The fitness function can be established defining for each parameter of instruction context a values scale. An example of the fitness function is presented in formula 10.
(10)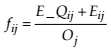
Where E_ Qij represents a value that indicates the level of knowledge that the learner i has in the Learning Unit j area, Eij represents the student’s experience in that area and Oj represents the occupancy degree of the considered learning unit.
Phase 2
The implementation of the adaptability property of the system is realised using a neural network, which has the goal to provide for each learner the proper teaching model. The neural network is trained, therefore an input vector involves a certain output. We define a value for acceptable error and we note it with ε .
We choose the structure of the neural network consisting of an input layer, a hidden layer and output layer and the standard connection (all neighbour layers are connected) (schema from Figure 14.2). The input layer has a number of units equal with the number of inputs. The input vector is defined by values which state the instruction context (MC, SC, TC, KC, CC,EC) (Moise, 2007)
Each context factor is defined by a set of parameters. Generalizing, the input vector is defined as in 11.
(11)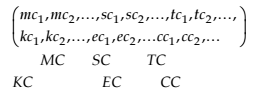
The output layer has more units (corresponding to the teaching models which conduct to maximal performance). The desired goal is to associate to each instruction context the proper model teaching. The number of units from the hidden layer can be chosen using a heuristic method or one can adjust it during the folding of the teaching process in order to increase the complexity of the network.
For instance, if we consider a neural network with d inputs and r outputs, we can select 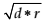 hidden units.
hidden units.
The neural network has to resolve the following problem: the association of an instruction context sacred to a learner with a teaching model obtained through the composition of the teaching models of each node from the conceptual map. Often, the architecture of the neural network remains fix and the values of weights are changed.
Schema of using the neural network in the instructional adaptive system is presented in Figure 14.6. We suppose that there are four teaching models (TM).
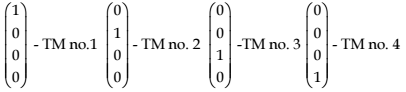
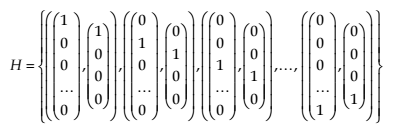
The inputs have the following forms:

The training set contains p pairs { knowninput,desired output}, hereupon we add perturbed inputs.
The error associated to the training set computed according to the formula 12.
(12)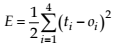
where oiis the current output and
ti is the desired output
The output of the neural network is computed as in formula 13.
(13)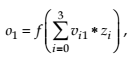
where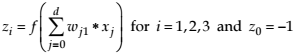
x0 =-1 are xj binary vectors
If 3=d , then the number of the hidden units is 3.
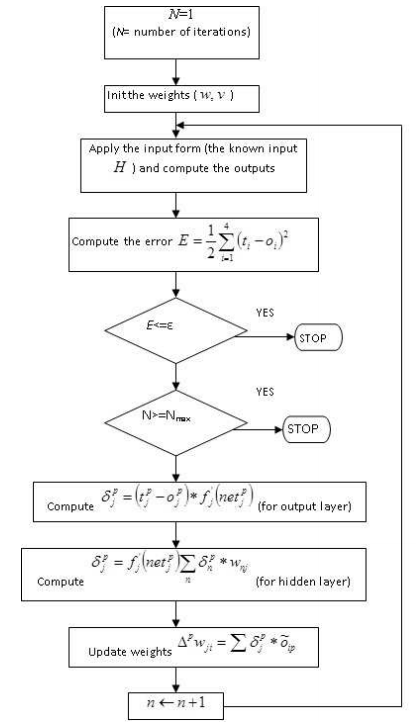
In order to adjust the weights, we use the backpropagation algorithm to train neural network presented in (**figure : The Backpropagation Algorithm).
- 2685 reads






