Neural networks are structures inspired from neuron circuits of the nervous systems and they are composed of interconnected computing units. Each neuron sends and receives impulses from other neurons and these changes are modelled as data changes. The main element of a neural network is the artificial neuron. Some indexes of neural networks development are the following: Warren McCulloch and Walter Pitts proposed the model in 1943 and it has still remained the fundamental unit of most of the neural networks. (McCulloch and Pitts, 1943) In 1958, Frank Rosenblatt added the learning abilities and developed the model of perceptron. (Rosenblatt, 1958) In 1986, David Rumelhart, Geoffrey Hinton and Ronald Williams defined a training algorithm for neural networks. (Rumelhart,Hinton, Williams, 1985) The diagram of a neuron with d inputs and one output is presented in Figure 14.1.
The main elements of a neural network that affects the functionality of the network are: the structure, the learning technique and the transfer function that reflects the way how the input is transferred to the output.
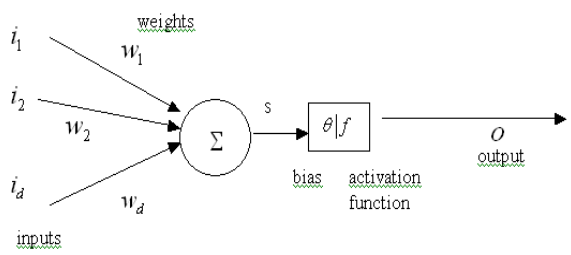
Each input has associated a synaptic weight, noted with w. This weight determines the effect of a certain input on the activation level of the neuron. The balanced sum of the inputs 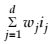 (called net input) defines the
activation of the neuron. The net input value is based on all input connections.
(called net input) defines the
activation of the neuron. The net input value is based on all input connections.
The net input can be calculated using the euclidian distance: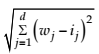
The function f represents the activation (or transfer) function and θ represents the bias. The output ( o ) is calculated using the following formula.
(1) 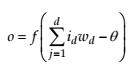
The most used forms of the activation function are presented in the formulas 2-6.
- step function
(2) 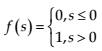
- signum function (used by Warren McCulloch and Walter Pitts)
(3)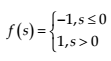
- linear function
(4)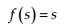
- sigmoid function
(5)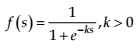
- generalized sigmoid function
(6)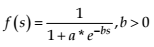
There are two fundamental structures for the neural networks: the feedforward neural network and the neural network with reaction. In the model proposed by Moise (Moise, 2010), it is used a feedforward neural network with a topology on levels, according to the geometrical positions of the neural units (Figure 14.2).
The model of a feedforward neural network with one input layer (with d units), one hidden layer (with p units), one output layer (with n units) and a linear activation function is described in formulas 7-8 (Figure 14.2).
(7)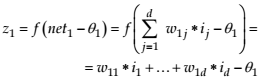
(8)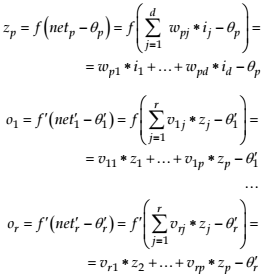
In the formulas 7-8, we considered that f (net)= f’(net) = net.
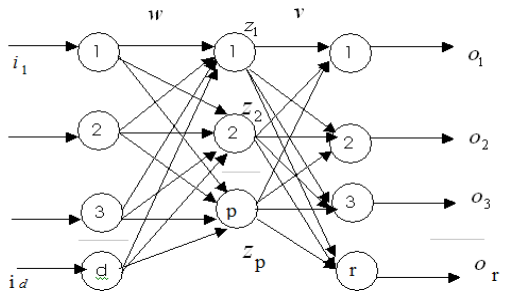
The positive weights determine the excitatory connections and the negative weights determine the inhibitory connections. The weights 0 denote the absence of connection between two neurons. The higher the absolute value of the weights (wj,i) is ,the influence of the neuron i on the neuron j is stronger. ) is, the stronger.
The neural networks are information processing adaptive systems. The most important quality of a neural network is its learning capacity. According to the received information, learning can be supervised or unsupervised. The supervised learning uses a training dataset, pairs of inputs and correct outputs. The algorithm used in the model of the e-learning system is the backpropagation algorithm and it works as follows: it computes the error as the difference between the desired output and the current output. The error is delivered back to the input of the neural network (Freeman, J. A., Skapura, 1991).
The performance function can be as in formula 9.
(9)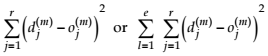
Where e represents the number of pairs (inputs, desired outputs), which form the training set.
The learning process of the neural network consists of two phases: one phase of learning and one phase of testing.
More details about the theory of a neural network can be found in (Freeman, J. A., Skapura, 1991).
The weights’ set that minimizes the error is the solution to the problem. Training of the neural network can be realized till the error decreases to an acceptable value or till reaches a maxim predefined epochs.
- 2591 reads






