Firms carrying very high risk do succeed in attracting investment through the capital market in the modern economy. In Silicon Valley ‘angel’ investors pour billions of dollars into startup companies that not only have no cash flow, but may also have no product! These start-ups frequently have no more than a good idea and are in need of financing in order to turn the idea into a product, and then bring the product to market.
 Capital market: a set of financial institutions
that funnels financing from investors into bonds and stocks.
Capital market: a set of financial institutions
that funnels financing from investors into bonds and stocks.
How can we reconcile the fact that, while these firms carry extraordinary uncertainty, investors are still willing to part with large sums of money to fund development? And the investors are not only billionaires with a good sense of the marketplace; private individuals who save for their retirement also invest in risky firms. These firms might not be start-ups, but every firm that has publicly-traded stocks is subject to major variations in its valuation.
The answer is that most individuals hold a portfolio of investments, which is a combination of different stocks and bonds. By investing in different stocks and bonds rather than concentrating in a narrow range of investments, an individual diversifies her portfolio. A rigourous theory underlies this “don’t put all of your eggs in the one basket” philosophy.
 Portfolio: a combination of assets that is
designed to secure an income from investing and to reduce risk.
Portfolio: a combination of assets that is
designed to secure an income from investing and to reduce risk.
We envisage investors as being risk-averse utility maximizers: An investor prefers higher average returns on his portfolio, but dislikes higher risk. To take on more risk, he needs to think he will get a higher average return. By “risk” here we mean the variability in the whole portfolio of assets. To highlight the essentials, let us keep things simple: He can invest his given amount of wealth in a safe and/or a risky asset. The higher the fraction in the risky asset, the greater is the average or expected return, but the greater the risk also.
The greater the risk associated with a given asset, the less of her money will a risk-averse individual invest in it. In general, she will switch more of her portfolio to the risky assets if these assets yield a higher return, or if their risk is lower.
Table 7.3 presents an example that is akin to the risk sharing undertaken by the IT consultant and his partner the musician. There are two risky shares here, Natural Gas (NG) and tech stocks (Tech). Each share is priced at $100 and each yields a $10 return in good times and $0 in bad times. The investor has $200 to invest, and each sector has a 50 percent probability (p=0.5) of good or bad times.
| Strategy | Expected returns with probabilities | Variance | ||
| $200 in NG | 220 (p=0.5) | 200 (p=0.5) | 100 | |
| $200 in Tech | 220 (p=0.5) | 200 (p=0.5) | 100 | |
| $100 in each | 220 (p=0.25) | 210 (p=0.25) | 200 (p=0.25) | 50 |
The outcomes from three different investment strategies are illustrated in Table 7.3. By investing all of her $200 in either NG or Tech, she will obtain $220 half of the time and $200 half of the time, as indicated in the first two outcome rows. But by diversifying through buying one of each stock, as illustrated in the final row, she reduces the variability of her portfolio. To see why, note that, since the performance of each stock is independent, there is now only a one chance in four that both stocks do well, and therefore there is a 25 percent probability of earning $220. By the same reasoning, there is a 25 percent probability of earning $200. But there is a 50 percent chance that one stock will perform well and the other poorly. When that happens, she gets a return of $210. In contrast to the outcomes defined in rows 1 and 2, the diversification strategy in row 3 yields fewer extreme outcomes and more outcomes that lie between the extremes.
 Diversification reduces the total risk of a
portfolio by pooling risks across several different assets whose individual returns behave independently.
Diversification reduces the total risk of a
portfolio by pooling risks across several different assets whose individual returns behave independently.
One way to measure the dispersion in outcomes is to calculate the variance associated with each strategy, and this is given in the final column. The variance is the weighted sum of the deviations between possible outcomes and the mean, squared.
 Variance is the weighted sum of the deviations
between all possible outcomes and the mean, squared.
Variance is the weighted sum of the deviations
between all possible outcomes and the mean, squared.
Mathematically:
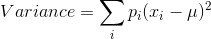
where 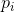 denotes the probability or weight associate with each
outcome i,
denotes the probability or weight associate with each
outcome i, 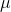 is the mean, or average, of the outcomes
is the mean, or average, of the outcomes 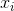 , and the capital sigma denotes the sum of such terms.
, and the capital sigma denotes the sum of such terms.
Consider now the variance in the example: The mean outcome is 210 with each strategy, it is a weighted average of each possible outcome. Since the values 220 and 200 each have a probability of one half, then the weighted average is clearly 210. Hence with strategy 1 the variance is
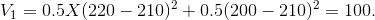
Strategy 2 yields the same value for the variance. But strategy 3 reduces the variance:
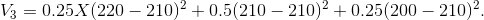
Hence 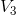 = 50.
= 50.
By diversifying her portfolio, the investor can reduce variability without necessarily reducing the average return! As we saw in Figure 7.1 less variability for the same average dollar return yields more utility on average. So diversification can increase utility on average.
Let us now push our example further in two very realistic ways. First, consider more extreme outcomes; second, consider the impact of having the option to invest in many firms rather than just two.
Rather than each share being valued at $110 or $100 at the end of the period, suppose the alternatives were $120 or $90. Note that the average return is unchanged. Despite the more extreme
outcomes, on average the portfolio still attains a value of $210 at the end of the investment period. In this case, the rewards for diversifying are even greater than before. Repeating the
calculations for the variance yields 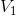 = 900,
= 900, 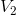 = 900, and
= 900, and 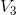 = 450. In reality stocks frequently double or triple in value in a short period of time, and firms go bankrupt, or almost, with
equal ease. In such a world the variance increases dramatically. Nonetheless there is a solution to the problem of high variance in the value of the portfolio – diversify further by adding more
stocks.
= 450. In reality stocks frequently double or triple in value in a short period of time, and firms go bankrupt, or almost, with
equal ease. In such a world the variance increases dramatically. Nonetheless there is a solution to the problem of high variance in the value of the portfolio – diversify further by adding more
stocks.
If we had four rather than just two equally risky stocks yielding the same average return, and the returns on each stock were independent of the returns on the others, then, by investing one-quarter of the available investment funds into each, the volatility of the portfolio, as measured by the variance, would be reduced. In this case we would invest $50 in each of four stocks rather than $100 in each of two. We need not proceed with the calculations.
Now, imagine that we had eight stocks, or 16, or 32, or 64. . . the “magic” of diversification is that the same average return can be attained, yet variability can be reduced. If it can be reduced sufficiently by adding ever more stocks to the portfolio, then even a very risk-averse individual can build a portfolio that is compatible with buying into risky firms. In essence, this is what mutual funds achieve.
At this point we may reasonably ask why individuals choose to invest any of their funds in the “safe” asset perhaps cash or government bonds. After all, if their return to bonds is significantly lower on average than the return to stocks, and they can diversify away much of the risk associated with stocks, why not get the higher average returns associated with stocks and put little nothing in the safer asset? The reason is that it is impossible to fully diversify. When a recession hits, for example, the whole stock market may take a dive, because profits fall across the whole economy. Because of this possibility, we cannot ever arrive at a portfolio where the returns to the different stocks are completely independent. As a consequence, the rational investor will decide to put some funds in bonds in order to reduce this systematic risk component that is associated with the whole market.
To see how the whole market can change dramatically students can go to any publicly accessible financial data site – such as Yahoo Finance and attempt to plot the TSX for the period 2005 – present, or the NASDAQ index from the mid-nineties to the present.
- 2917 reads






