Economists have a particular liking for competitive markets. The reason is not, as is frequently thought, that we love competitive battles; it really concerns resource allocation in the economy at large. In Chapter 5 we explained why markets are an excellent vehicle for transporting the economy’s resources to where they are most valued: a perfectly competitive marketplace in which there are no externalities results in resources being used up to the point where the demand and supply prices are equal. If demand is a measure of marginal benefit and supply is a measure of marginal cost, then a perfectly competitive market insures that this condition will hold in equilibrium. Perfect competition, therefore, results in resources being used efficiently.
Our initial reaction to this perspective may be: If market equilibrium is such that the quantity supplied always equals the quantity demanded, is not every market efficient? The answer is no. As we shall see in the next chapter on monopoly, the monopolist’s supply decision does not reflect the marginal cost of resources used in production, and therefore does not result in an efficient allocation in the economy.
KEY TERMS
Perfect competition: an industry in which many suppliers, producing an identical product, face many buyers, and no one participant can influence the market.
Profit maximization is the goal of competitive suppliers – they seek to maximize the difference between revenues and costs.
The short run is a period during which the number of firms and their plant sizes are fixed.
The long run is a sufficiently long period of time to permit entry and exit and for firms to change their plant size.
Marginal revenue is the additional revenue accruing to the firm resulting from the sale of one more unit of output.
Shut-down price corresponds to the minimum value of the AVC curve.
Break-even price corresponds to the minimum of the ATC curve.
Short-run supply curve for perfect competitor: the portion of the MC curve above the minimum of the AVC.
Industry supply (short run) in perfect competition is the horizontal sum of all firms’ supply curves.
Short run equilibrium in perfect competition occurs when each firm maximizes profit by producing a quantity where P = MC.
Normal profits are required to induce suppliers to supply their goods and services. They reflect opportunity costs and can therefore be considered as a type of cost
component.
Economic (supernormal) profits are those profits above normal profits that induce firms to enter an industry. Economic profits are based on the opportunity cost of the
resources used in production.
Accounting profits are the difference between revenues and actual costs incurred.
Long-run equilibrium in a competitive industry requires a price equal to the minimum point of a firm’s ATC. At this point, only normal profits exist, and there is no
incentive for firms to enter or exit.
Industry supply in the long-run in perfect competition is horizontal at a price corresponding to the minimum of the representative firm’s long-run ATC curve.
Increasing (decreasing) cost industry is one where costs rise (fall) for each firm because of the scale of industry operation.
EXERCISES
- Wendy’s Window Cleaning is a small local operation. Winnie presently cleans the outside windows in her neighbours’ houses for $36 per house. She does ten houses per day. She
is incurring total costs of $420, and of this amount $100 is fixed. The cost per house is constant.
- What is the marginal cost associated with cleaning the windows of one house – we know it is constant?
- At a price of $36, what is her break-even level of output (number of houses)?
- If the fixed cost is ‘sunk’ and she cannot increase her output in the short run, should she shut down?
- A manufacturer of vacuum cleaners incurs a constant variable cost of production equal to $80. She can sell the appliances to a wholesaler for $130. Her annual fixed costs are $200,000. How many vacuums must she sell in order to cover her total costs?
- For the vacuum cleaner producer in the preceding question:
- Draw the MC curve.
- Next, draw her AFC and her AVC curves.
- Finally, draw her ATC curve.
- In order for this cost structure to be compatible with a perfectly competitive industry, what must happen to her MC curve at some output level?
- Consider the supply curves of two firms in a competitive industry: P =
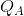 and P = 2
and P = 2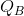 .
.
- On a diagram, draw these two supply curves, marking their intercepts and slopes numerically (remember that they are really MC curves).
- Now draw a supply curve that represents the combined supply of these two firms.
- Amanda’s Apple Orchard Productions Limited produces 10,000 kilograms of apples per month. Her total production costs at this output level are $8,000. Two of her many
competitors have larger-scale operations and produce 12,000 and 15,000 kilos at total costs of $9,500 and $11,000 respectively. If this industry is competitive, on what segment of the LAC
curve are these producers producing?
- Consider the data in the table below. TC is total cost, TR is total revenue, and Q is output.
Q 0 1 2 3 4 5 6 7 8 9 10 TC 10 18 24 31 39 48 58 69 82 100 120 TR 0 11 22 33 44 55 66 77 88 99 110 - Add some extra rows to the table below and for each level of output calculate the MR, the MC and total profit.
- Next, compute AFC, AVC, and ATC for each output level, and draw these three cost curves on a diagram.
- What is the profit-maximizing output?
- How can you tell that this firm is in a competitive industry?
- The market demand and supply curves in a perfectly competitive industry are given by: Qd = 30,000 - 600P and Qs = 200P - 2000.
- Draw these functions on a diagram, and calculate the equilibrium price of output in this industry.
- Now assume that an additional firm is considering entering. This firm has a short-run MC curve defined by MC = 10+0.5Q, where Q is the firm’s output. If this firm enters the industry and it knows the equilibrium price in the industry, what output should it produce?
- Consider the preceding question again.
- Suppose all of the existing firms have the same cost structure as the new entrant, how many firms are there in the industry?
- Each firm in the industry has a total cost curve of the form TC =400+10Q+(1/4)
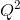 . There is no distinction between the long run and short run – there is only one possible size of firm. Derive the ATC by
dividing each term in the TC curve by Q, and calculate the cost per unit at the output being produced by each firm at the existing equilibrium price.
. There is no distinction between the long run and short run – there is only one possible size of firm. Derive the ATC by
dividing each term in the TC curve by Q, and calculate the cost per unit at the output being produced by each firm at the existing equilibrium price.
- Since you now know the price and cost per unit, calculate the profit that each firm is making.
- Is the ATC sloping up or down at the current equilibrium? [Hint: is the MC above or below the ATC at the chosen output?]
- Consider the long-run for the industry described in the preceding question.
- What will happen to the number of firms in this industry in the long run?
- The minimum of the ATC curve for this firm occurs at a value of $30. Given that you know this, what output will be produced in the industry in the long run?
- Once you know the output produced in the industry, and the minimum of the ATC curve, calculate the number of firms that will produce in the long run ‘normal profit’ equilibrium.
- Now consider what will happen in this industry in the very long run – with technological change. The total cost curve becomes TC = 225+10Q+(1/4)
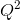 . The MC remains unchanged, and the minimum of the ATC now occurs at a value of $25.
. The MC remains unchanged, and the minimum of the ATC now occurs at a value of $25.
- What is the price in the market in this new long run, and what quantity is traded?
- What quantity will each firm produce at this price?
- How many firms will there be in the industry?
- Consider two firms in a perfectly competitive industry. They have the same MC curves and differ only in having higher and lower fixed costs. Suppose the ATC curves are of the
form: 400/Q+10+(1/4)Q and 225/Q+10+(1/4)Q. The MC for each is a straight line: MC = 10+(1/2)Q.
- Each ATC curve is U shaped and has a minimum at the quantities 40 and 30 respectively. Draw two ATC curve on the same diagram as the MC curve that reflect this information.
- Compute the break-even price for each firm.
- Explain why both of these firms cannot continue to produce in the long run in a perfectly competitive market.
- Could you derive an expression for the total variable cost curve for these firms, given the total cost curves are: 400+10Q+(1/4)
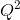 , and 225+10Q+(1/4)
, and 225+10Q+(1/4)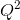 ?
?
- 4496 reads






