We are now in a position to make a general statement about the relative output levels that will be produced in several different market structures when marginal costs are constant. For ease of exposition we use the foregoing numerical example, where the market demand is given by P = 24 - Q, and MC = 6.
In the duopoly case we saw that the output for each firm i (assumed identical) was 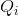 = 6.
= 6.
With monopoly, profit is maximized where MC =MR. Since MR = 24 - 2Q, the monopoly output is obtained from the equation 6 = 24 - 2Q; that is Q = 9.
If these two firms acted in the same way as perfect competitors (we cannot call this perfect competition because there are just two firms), we know from Perfect competition that the market solution is where
P = MC. Consequently, if we equate the demand and MC functions the solution for the market outcome is Q = 18 (equating 24 - Q = 6 yields Q = 18).
In this case of constant marginal costs, the above solutions indicate that we can formulate a general rule regarding the output of firms that depends on the number of firms N.
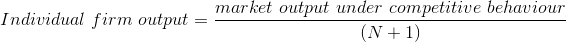
For example, in the duopoly case, substituting N = 2 and competitive output of 18 yields a firm output of 6. In the monopoly case N = 1 and hence output is 9.
- 1918 reads






