Monopoly and perfect competition are interesting paradigms; but few markets resemble them in the real world. In this chapter we addressed some of the complexities that define the world around us: it is characterized by strategic planning, entry deterrence, differentiated products and so forth.
Entry and exit are critical to competitive markets. Frequently entry is blocked because of scale economies – an example of a natural or unintended entry barrier. In addition, incumbents can formulate strategies to limit entry, for example by investing in additional capacity or in the development of new products. Such strategies, where effective, are called credible threats.
We also stress that firms act strategically – particularly whenever there are just a few participants present. Before taking any action, these firms make conjectures about how their competitors will react, and incorporate such reactions into their planning. Competition between suppliers can frequently be defined in terms of a game, and such games usually have an equilibrium outcome.
The Cournot duopoly model that we developed is a game between two competitors in which an equilibrium market output is determined from a pair of reaction functions. Scale economies are critical. Large development costs or set up costs mean that the market will generally support just a limited number of producers. In turn this implies that potential new (smallscale) firms cannot benefit from the scale economies and will not survive competition from largescale suppliers.
Finally, product differentiation is critical. If small differences exist between products produced in markets where there is free entry we get a monopolistically competitive market. In these markets long run profits are ‘normal’ and firms operate with some excess capacity. It is not possible to act strategically in this kind of market.
KEY TERMS
Imperfectly competitive firms face a downward-sloping demand curve, and their output price reflects the quantity sold.
Oligopoly defines an industry with a small number of suppliers.
Monopolistic competition defines a market with many sellers of products that have similar characteristics. Monopolistically competitive firms can exert only a small influence
on the whole market.
Duopoly defines a market or sector with just two firms.
Concentration ratio: N-firm concentration ratio is the sales share of the largest N firms in that sector of the economy.
Differentiated product is one that differs slightly from other products in the same market.
The monopolistically competitive equilibrium in the long run requires the firm’s demand curve to be tangent to the ATC curve at the output where MR = MC.
Collusion is an explicit or implicit agreement to avoid competition with a view to increasing profit.
Conjecture: a belief that one firm forms about the strategic reaction of another competing firm.
Game: a situation in which contestants plan strategically to maximize their profits, taking account of rivals’ behaviour.
Strategy: a game plan describing how a player acts, or moves, in each possible situation.
Nash equilibrium: one in which each player chooses the best strategy, given the strategies chosen by the other player, and there is no incentive for any player to move.
Dominant strategy: a player’s best strategy, whatever the strategies adopted by rivals.
Payoff matrix: defines the rewards to each player resulting from particular choices.
Binding commitment: an agreement, entered into voluntarily, that restricts future actions.
Credible threat: one that, after the fact, is still optimal to implement.
Cournot behaviour involves each firm reacting optimally in their choice of output to their competitors’ decisions.
Reaction functions define the optimal choice of output conditional upon a rival’s output choice.
EXERCISES
- Imagine that the biggest four firms in each of the sectors listed below produce the amounts defined in each cell. Compute the three-firm and four-firm concentration ratios for each sector, and rank the sectors by degree of industry concentration.
- You own a company in a monopolistically competitive market. Your marginal cost of production is $12 per unit. There are no fixed costs. The demand for your own product is
given by the equation P = 48 - (1/2)Q.
- Plot the demand curve, the marginal revenue curve, and the marginal cost curve.
- Compute the profit-maximizing output and price combination.
- Compute total revenue and total profit.
- In this monopolistically competitive industry, can these profits continue indefinitely?
- Two firms in a particular industry face a market demand curve given by the equation P = 100 - (1/3)Q. The marginal cost is $40 per unit and the marginal revenue is MR =
100(2/3)Q.
- Draw the demand curve to scale on a diagram, and then insert the corresponding marginal revenue curve and the MC curve.
- If these firms got together to form a cartel, what output would they produce and what price would they charge?
- Assuming they each produce half of the total what is their individual profit?
- Suppose now that one of the firms in the previous question decides to break the cartel agreement and makes a decision to sell 10 additional units.
- How many units does he intend to sell?
- If the other supplier maintains her output at the cartel level, at what price will the new total output be sold?
- What profit will each make in this new situation?
- Is the combined profit here greater or less than in the cartel situation?
- How is the firm that previously maintained the cartel output level likely to react here?
- The classic game theory problem is the “prisoners’ dilemma.” In this game, two criminals are apprehended, but the police have only got circumstantial evidence to prosecute
them for a small crime, without having the evidence to prosecute them for the major crime of which they are suspected. The interrogators then pose incentives to the crooks-incentives to talk.
The crooks are put in separate jail cells and have the option to confess or deny. Their payoff depends upon what course of action each adopts. The payoff matrix is given below. The first
element in each box is the payoff (years in jail) to the player in the left column, and the second element is the payoff to the player in the top row.
- Does a “dominant strategy” present itself for each or both of the crooks?
- What is the Nash equilibrium to this game?
- Is the Nash equilibrium unique?
- Was it important for the police to place the crooks in separate cells?
- Taylormade and Titlelist are considering a production strategy for their new golf drivers. If they each produce a small output, they can price the product higher and make more
profit than if they each produce a large output. Their payoff/profit matrix is given below.
- Does either player have a dominant strategy here?
- What is the Nash equilibrium to the game?
- Do you think that a cartel arrangement would be sustainable?
- The reaction functions for two firms A and B in a duopoly are given by:
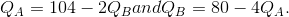
- Plot the reaction functions to scale on a graph.
- Solve the two reaction functions for the equilibrium output produced by each.
- Do you think that these firms have the same cost structure? Explain.
- Consider the example developed in Duopoly
and Cournot games, assuming this time that firm A has a MC of $4 per unit, and B has a MC of $6.
- Compute the level of output each will produce
- Compute the total output produced by both firms.
- Compute the profit made by each firm.
- Comparing their combined output with the output when the MC of each firm is $6, explain why the totals differ.
- Consider the market demand curve for appliances: P = 3,200 - (1/4)Q. There are no fixed production costs, and the marginal cost of each appliance is MC = $400.
- Determine the output that will be produced in a ‘perfectly competitive’ market structure where no profits accrue in equilibrium.
- If this market is supplied by a monopolist what is the profit maximizing output?
- What will be the total output produced in the Cournot duopoly game? [Hint: you can either derive the reaction functions and solve them, or use the formula from Section 10.6 of the chapter.]
- Consider the outputs you have obtained in the preceding question.
- Compute the profit levels under each of the three market structures.
- Can you figure out how many firms would produce at the perfectly competitive output? If not, can you think of a reason?
- Ronnie’s Wraps is the only supplier of sandwich food and makes a healthy profit. It currently charges a high price and makes a profit of six units. However, Flash Salads is
considering entering the same market. The payoff matrix below defines the profit outcomes for different possibilities. The first entry in each cell is the payoff/profit to Flash Salads and
the second to Ronnie’s Wraps.
Ronnie’s Wraps High price Low price Flash Salads Enter the market 2,3 -1,1 Stay out of market 0,6 0.4 - If Ronnie’s Wraps threatens to lower its price in response to the entry of a new competitor, should Flash Salads stay away or enter?
- Explain the importance of threat credibility here.
- A monopolistically competitive firm has an average total cost curve given by ATC = 2/Q+ 1+Q/8. The slope of this curve is given by
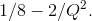 The marginal cost isMC =1+Q/4. Her demand curve is given by P = 3-(3/8)Q, and so the
marginal revenue curve is given by MR = 3 - (3/4)Q. We know that the equilibrium for this firm (see Figure 11.2) is where the demand curve is tangent to the ATC
curve – where the slopes are equal.
The marginal cost isMC =1+Q/4. Her demand curve is given by P = 3-(3/8)Q, and so the
marginal revenue curve is given by MR = 3 - (3/4)Q. We know that the equilibrium for this firm (see Figure 11.2) is where the demand curve is tangent to the ATC
curve – where the slopes are equal.
- What is the equilibrium output for this firm [Hint: find where the slope of the demand curve equals the slope of the ATC curve]?
- At what price will the producer sell this output?
- Solve for where MC =MR, this is the profit maximizing condition – does it correspond to where the slope of the demand curve equals the slope of the ATC?
- Since the MC always intersects the ATC at the minimum of the ATC, solve for the output level that defines this ATC minimum.
- 4391 reads






