Just as there is a relationship between the marginal and average cost curves in the short run, there is a complementary relationship between the two in the long run also. In the long run all
costs are variable. Hence, the long run marginal cost (LMC) is defined as the increment in cost associated with producing one more unit of output when all inputs are adjusted in a cost
minimizing manner.
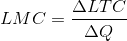
 Long run marginal cost is the increment in
cost associated with producing one more unit of output when all inputs are adjusted in a cost minimizing manner.
Long run marginal cost is the increment in
cost associated with producing one more unit of output when all inputs are adjusted in a cost minimizing manner.
Figure 8.6 illustrates a LMC curve where there are initially declining marginal costs, then constant marginal costs and finally increasing marginal costs. The associated data are presented in Table 8.3. This example has been constructed with three linear segments to the LMC curve in order to show the relationship between returns to scale and long run marginal costs: the LATC still has a smooth U shape, and intersects the LMC at the minimum of the LATC. The logic for this occurrence is precisely as in the short run case: whenever the marginal cost is less than the average cost the latter must fall, and conversely when the marginal cost is greater than the average cost.
| Output | LMC | LAC | Scale |
| 0 | 80 | 80.00 | Increasing returns to scale |
| 100 | 72 | 76.00 | |
| 200 | 64 | 72.00 | |
| 300 | 56 | 68.00 | |
| 400 | 48 | 64.00 | |
| 500 | 40 | 60.00 | |
| 600 | 40 | 56.67 | |
| 700 | 40 | 54.29 | |
| 800 | 40 | 52.50 | |
| 900 | 40 | 51.11 | |
| 1000 | 40 | 50.00 | |
| 1100 | 44 | 49.27 | |
| 1200 | 48 | 49.00 | |
| 1300 | 52 | 49.08 | Decreasing returns to scale |
| 1400 | 56 | 49.43 | |
| 1500 | 60 | 50.00 | |
| 1600 | 64 | 50.75 | |
| 1700 | 68 | 51.65 | |
| 1800 | 72 | 52.67 | |
| 1900 | 76 | 53.79 | |
| 2000 | 80 | 55.00 |
- 4909 reads






