Complex Exponentials

Available under Creative Commons-ShareAlike 4.0 International License.

The most important signal is complex-valued, the complex exponential.

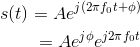
$\begin{align*} s(t)=Ae^{j(2\pi f_0t+\phi)}\\ =Ae^{j\phi}e^{j2\pi f_0t}\\ \end{align*}$

Here, j denotes 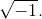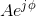$\sqrt{-1}.$ $Ae^{j\phi}$ is known as the signal's complex amplitude. Considering the complex amplitude as a complex number in polar form, its magnitude is the amplitude A and its angle the signal phase. The complex amplitude is also known as a phasor. The complex exponential cannot be further decomposed into more elemental signals, and is the most important signal in electrical engineering! Mathematical manipulations at first appear to be more difficult because complex-valued numbers are introduced. In fact, early in the twentieth century, mathematicians thought engineers would not be sufficiently sophisticated to handle complex exponentials even though they greatly simplified solving circuit problems. Steinmetz 5 introduced complex exponentials to electrical engineering, and demonstrated that "mere" engineers could use them to good effect and even obtain right answers! See Complex Numbers for a review of complex numbers and complex arithmetic.

The complex exponential defines the notion of frequency: it is the only signal that contains only one frequency component. The sinusoid consists of two frequency components: one at the frequency +f₀ and the other at −f₀.

EULER RELATION: This decomposition of the sinusoid can be traced to Euler's relation.

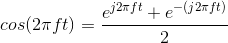
$cos(2\pi ft)=\frac{e^{j2\pi ft}+e^{-(j2\pi ft)}}{2}$
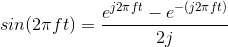
$sin(2\pi ft)=\frac{e^{j2\pi ft}-e^{-(j2\pi ft)}}{2j}$
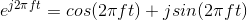
$e^{j2\pi ft}=cos(2\pi ft)+jsin(2\pi ft)$

DECOMPOSITION: The complex exponential signal can thus be written in terms of its real and imaginary parts using Euler's relation. Thus, sinusoidal signals can be expressed as either the real or the imaginary part of a complex exponential signal, the choice depending on whether cosine or sine phase is needed, or as the sum of two complex exponentials. These two decompositions are mathematically equivalent to each other.

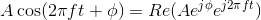
$A\cos(2\pi ft+\phi)=Re(Ae^{j\phi }e^{j2\pi ft})$
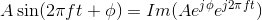
$A\sin(2\pi ft+\phi)=Im(Ae^{j\phi }e^{j2\pi ft})$

Using the complex plane, we can envision the complex exponential's temporal variations as seen in the above Figure 2.2. The magnitude of the complex exponential is A, and the initial value of the complex exponential at t =0 has an angle of φ. As time increases, the locus of points traced by the complex exponential is a circle (it has constant magnitude of A). The number of times per second we go around the circle equals the frequency f. The time taken for the complex exponential to go around the circle once is known as its period T, and equals 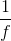$\frac{1}{f}$ . The projections onto the real and imaginary axes of the rotating vector representing the complex exponential signal are the cosine and sine signal of Euler's relation ((2.16)).

1663 reads

You are here

Complex Exponentials