Real Exponentials

Available under Creative Commons-ShareAlike 4.0 International License.

As opposed to complex exponentials which oscillate, real exponentials (Figure 2.3) decay.

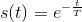
$s(t)=e^{-\frac{t}{T}}$

The quantity τ is known as the exponential's time constant, and corresponds to the time required for the exponential to decrease by a factor of $\frac{1}{e}$ , which approximately equals 0.368. A decaying complex exponential is the product of a real and a complex exponential.

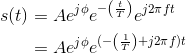
$\begin{align*} s(t)&=Ae^{j\phi}e^{-\left ( \frac{t}{T} \right )}e^{j2\pi ft}\\ &=Ae^{j\phi}e^{(-\left ( \frac{1}{T} \right )+j2\pi f)t}\\ \end{align*}$

In the complex plane, this signal corresponds to an exponential spiral. For such signals, we can define complex frequency as the quantity multiplying t.

1250 reads

You are here

Real Exponentials