Series and Parallel Circuits

Available under Creative Commons-ShareAlike 4.0 International License.

Figure 3.8 Circult examples

The circuit shown is perhaps the simplest circuit that performs a signal processing function. The input is provided by the voltage source v_in and the output is the voltage v_out across the resistor labelled R₂

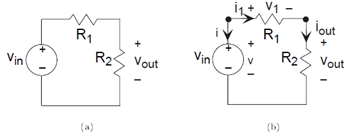
The results shown in other modules (Electric Circuits and Interconnection Laws, KVL and KCL, interconnection laws) with regard to this circuit (Figure 3.8), and the values of other currents and voltages in this circuit as well, have profound implications.

Resistors connected in such a way that current from one must flow only into another currents in all resistors connected this way have the same magnitude are said to be connected in series. For the two series-connected resistors in the example, the voltage across one resistor equals the ratio of that resistor's value and the sum of resistances times the voltage across the series combination. This concept is so pervasive it has a name: voltage divider.

The input-output relationship for this system, found in this particular case by voltage divider, takes the form of a ratio of the output voltage to the input voltage.

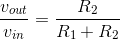
$\frac{v_{out}}{v_{in}}=\frac{R_2}{R_1+R_2}$

In this way, we express how the components used to build the system affect the input-output relationship. Because this analysis was made with ideal circuit elements, we might expect this relation to break down if the input amplitude is too high (Will the circuit survive if the input changes from 1 volt to one million volts?) or if the source's frequency becomes too high. In any case, this important way of expressing input-output relationships as a ratio of output to input pervades circuit and system theory.

The current i₁ is the current flowing out of the voltage source. Because it equals i₂, we have that

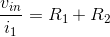
$\frac{v_{in}}{i_1}=R_1+R_2$

RESISTORS IN SERIES: The series combination of two resistors acts, as far as the voltage source is concerned, as a single resistor having a value equal to the sum of the two resistances.

This result is the first of several equivalent circuit ideas: In many cases, a complicated circuit when viewed from its terminals (the two places to which you might attach a source) appears to be a single circuit element (at best) or a simple combination of elements at worst. Thus, the equivalent circuit for a series combination of resistors is a single resistor having a resistance equal to the sum of its component resistances.

Figure 3.9 Resistors

The resistor (on the right) is equivalent to the two resistors (on the left) and has a resistance equal to the sum of the resistances of the other two resistors.

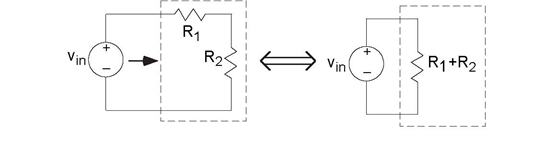
Thus, the circuit the voltage source "feels" (through the current drawn from it) is a single resistor having resistance R₁ + R₂. Note that in making this equivalent circuit, the output voltage can no longer be defined: The output resistor labeled R₂ no longer appears. Thus, this equivalence is made strictly from the voltage source's viewpoint.

:

Figure 3.10 A simple parallel circuit.

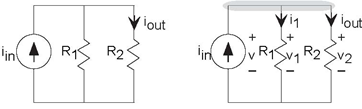
One interesting simple circuit (Figure 3.10) has two resistors connected side-by-side, what we will term a parallel connection, rather than in series. Here, applying KVL reveals that all the voltages are identical: v₁ = v and v₂ = v. This result typifies parallel connections. To write the KCL equation, note that the top node consists of the entire upper interconnection section. The KCL equation is i_in − i₁ − i₂ =0. Using the v-i relations, we find that

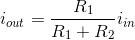
$i_{out}=\frac{R_1}{R_1+R_2}i_{in}$

Exercise 3.6.1

Suppose that you replaced the current source in Figure 3.10 by a voltage source. How would i_out be related to the source voltage? Based on this result, what purpose does this revised circuit have? This circuit highlights some important properties of parallel circuits. You can easily show that the parallel combination of R₁ and R₂ has the v-i relation of a resistor having resistance 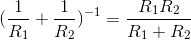$(\frac{1}{R_1}+\frac{1}{R_2})^{-1}=\frac{R_1R_2}{R_1+R_2}$ . A notation for this quantity is ( R₁ || R₂). As the reciprocal of resistance is conductance (Resistor ), we can say that for a parallel combination of resistors, the equivalent conductance is the sum of the conductances.

Figure 3.11 A parallel combination of resistors

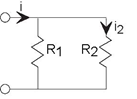
Similar to voltage divider for series resistances, we have current divider for parallel resistances. The current through a resistor in parallel with another is the ratio of the conductance of the first to the sum of the conductances. Thus, for the depicted circuit,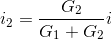 $i_2=\frac{G_2}{G_1+G_2}i$ . 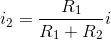Expressed in terms of resistances, current divider takes the form of the resistance of the other resistor divided by the sum of resistances: $i_2=\frac{R_1}{R_1+R_2}i$

Figure 3.12 Circult example 2

:

Figure 3.13 Circuit example 3

The simple attenuator circuit is attached to an oscilloscope's input. The input-output relation for the above circuit without a load is: .

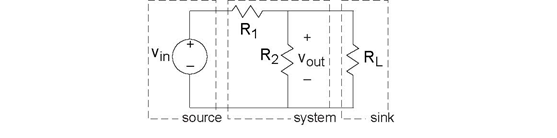
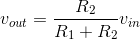
$v_{out}=\frac{R_{2}}{R_{1}+R_{2}}v_{in}$

Suppose we want to pass the output signal into a voltage measurement device, such as an oscilloscope or a voltmeter. In system-theory terms, we want to pass our circuit's output to a sink. For most applications, we can represent these measurement devices as a resistor, with the current passing through it driving the measurement device through some type of display. In circuits, a sink is called a load; thus, we describe a system-theoretic sink as a load resistance R_L. Thus, we have a complete system built from a cascade of three systems: a source, a signal processing system (simple as it is), and a sink.

We must analyze afresh how this revised circuit, shown in Figure 3.13, works. Rather than defining eight variables and solving for the current in the load resistor, let's take a hint from other analysis (series rules, parallel rules). Resistors R₂ and R_L are in a parallel configuration: The voltages across each resistor are the same while the currents are not. 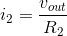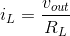Because the voltages are the same, we can find the current through each from their v-i relations: $i_2=\frac{v_{out}}{R_2}$ and $i_L=\frac{v_{out}}{R_L}$ . Considering the node where all three resistors join, KCL says that the sum of the three currents must equal zero. Said another way, the current entering the node through R1 must equal the sum of the other two currents leaving the node. 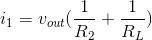Therefore, i₁ = i₂ + i_L, which means that $i_1=v_{out}(\frac{1}{R_2}+\frac{1}{R_L})$

Let R_eq denote the equivalent resistance of the parallel combination of R₂ and R_L. Using R1'sv-i relation, the voltage across it is 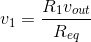$v_1=\frac{R_1v_{out}}{R_{eq}}$ . The KVL equation written around the leftmost loop has v_in= v₁ + v_out ; substituting for v₁, we find

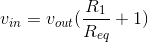
$v_{in}=v_{out}(\frac{R_1}{R_{eq}}+1)$
or
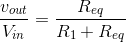
$\frac{v_{out}}{V_{in}}=\frac{R_{eq}}{R_1+R_{eq}}$

Thus, we have the input-output relationship for our entire system having the form of voltage divider, but it does not equal the input-output relation of the circuit without the voltage measurement device. We can not measure voltages reliably unless the measurement device has little effect on what we are trying to measure. We should look more carefully to determine if any values for the load resistance would lessen its impact on the circuit. 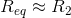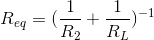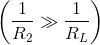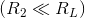Comparing the input-output relations before and after, what we need is $R_{eq}\approx R_2$ As $R_{eq}=(\frac{1}{R_2}+\frac{1}{R_L})^{-1}$ , the approximation would apply if $\left ( \frac{1}{R_{2}}\gg \frac{1}{R_{L}} \right )$ or $\left ( R_{2} \ll R_{L}\right )$ This is the condition we seek:

VOLTAGE MEASUREMENT: Voltage measurement devices must have large resistances compared with that of the resistor across which the voltage is to be measured.

Exercise 3.6.2

Let's be more precise: How much larger would a load resistance need to be to affect the input-output relation by less than 10%? by less than 1%?

Example 3.1

Figure 3.14 Example 3.1

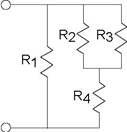
We want to find the total resistance of the example circuit. To apply the series and parallel combination rules, it is best to first determine the circuit's structure: What is in series with what and what is in parallel with what at both small-and large-scale views. We have R₂ in parallel with R₃; this combination is in series with R₄. This series combination is in parallel with R₁. Note that in determining this structure, we started away from the terminals, and worked toward them. In most cases, this approach works well; try it first. The total resistance expression mimics the structure:

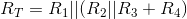
R_T=R_1||(R_2||R_3+R_4)
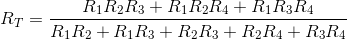
$R_T=\frac{R_1R_2R_3+R_1R_2R_4+R_1R_3R_4}{R_1R_2+R_1R_3+R_2R_3+R_2R_4+R_3R_4}$
Such complicated expressions typify circuit "simplifications." A simple check for accuracy is the units: Each component of the numerator should have the same units (here Ω³) as well as in the denominator (Ω²). The entire expression is to have units of resistance; thus, the ratio of the numerator's and denominator's units should be ohms. Checking units does not guarantee accuracy, but can catch many errors.

Another valuable lesson emerges from this example concerning the difference between cascading systems and cascading circuits. In system theory, systems can be cascaded without changing the input-output relation of intermediate systems. In cascading circuits, this ideal is rarely true unless the circuits are so designed. Design is in the hands of the engineer; he or she must recognize what have come to be known as loading effects. In our simple circuit, you might think that making the resistance R_L large enough would do the trick. Because the resistors R₁ and R₂ can have virtually any value, you can never make the resistance of your voltage measurement device big enough. Said another way, a circuit cannot be designed in isolation that will work in cascade with all other circuits. Electrical engineers deal with this situation through the notion of specifications: Under what conditions will the circuit perform as designed? Thus, you will find that oscilloscopes and voltmeters have their internal resistances clearly stated, enabling you to determine whether the voltage you measure closely equals what was present before they were attached to your circuit. Furthermore, since our resistor circuit functions as an attenuator, with the attenuation (a fancy word for gains less than one) depending only on the ratio of the two resist or values 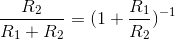$\frac{R_2}{R_1+R_2}=(1+\frac{R_1}{R_2})^{-1}$ , we can select any values for the two resistances we want to achieve the desired attenuation. The designer of this circuit must thus specify not only what the attenuation is, but also the resistance values employed so that integrators people who put systems together from component systems can combine systems together and have a chance of the combination working.

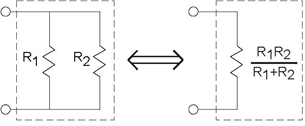
Figure 3.15 summarizes the series and parallel combination results. These results are easy to remember and very useful. Keep in mind that for series combinations, voltage and resistance are the key quantities, while for parallel combinations current and conductance are more important. In series combinations, the currents through each element are the same; in parallel ones, the voltages are the same.

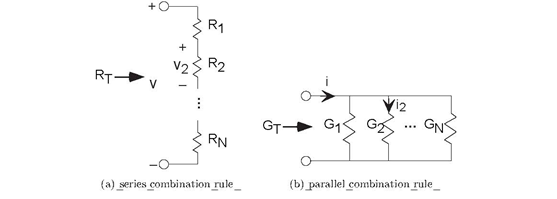
Figure 3.15 Series a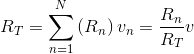nd parallel combonation rules

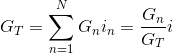
(a) $R_{T}=\sum_{n=1}^{N}\left ( R_{n} \right )v_{n}=\frac{R_{n}}{R_{T}}v$ (b) $G_{T}=\sum_{n=1}^{N}G_{n}i_{n}=\frac{G_{n}}{G_{T}}i$

Exercise 3.6.3

Contrast a series combination of resistors with a parallel one. Which variable (voltage or current) is the same for each and which differs? What are the equivalent resistances? When resistors are placed in series, is the equivalent resistance bigger, in between, or smaller than the component resistances? What is this relationship for a parallel combination?

3351 reads

You are here

Series and Parallel Circuits