In many situations, it is useful to have a way to describe the location of an individual score within its distribution. One approach is the percentile rank. The percentile rank of a score is the percentage of scores in the distribution that are lower than that score. Consider, for example, the distribution in Table 12.1. For any score in the distribution, we can find its percentile rank by counting the number of scores in the distribution that are lower than that score and converting that number to a percentage of the total number of scores. Notice, for example, that five of the students represented by the data in Table 12.1 had self-esteem scores of 23. In this distribution, 32 of the 40 scores (80%) are lower than 23. Thus each of these students has a percentile rank of 80. (It can also be said that they scored “at the 80th percentile.”) Percentile ranks are often used to report the results of standardized tests of ability or achievement. If your percentile rank on a test of verbal ability were 40, for example, this would mean that you scored higher than 40% of the people who took the test.
Another approach is the zscore. The z score for a particular individual is the difference between that individual’s score and the mean of the distribution, divided by the standard deviation of the distribution:
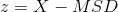
A z score indicates how far above or below the mean a raw score is, but it expresses this in terms of the standard deviation. For example, in a distribution of intelligence quotient (IQ) scores with a mean of 100 and a standard deviation of 15, an IQ score of 110 would have a zscore of (110 − 100) / 15 = +0.67. In other words, a score of 110 is 0.67 standard deviations (approximately two thirds of a standard deviation) above the mean. Similarly, a raw score of 85 would have a zscore of (85 − 100) / 15 = −1.00. In other words, a score of 85 is one standard deviation below the mean.
There are several reasons that zscores are important. Again, they provide a way of describing where an individual’s score is located within a distribution and are sometimes used to report the results of standardized tests. They also provide one way of defining outliers. For example, outliers are sometimes defined as scores that have zscores less than −3.00 or greater than +3.00. In other words, they are defined as scores that are more than three standard deviations from the mean. Finally, zscores play an important role in understanding and computing other statistics, as we will see shortly.
Online Descriptive Statistics
Although many researchers use commercially available software such as SPSS and Excel to analyze their data, there are several free online analysis tools that can also be extremely useful. Many allow you to enter or upload your data and then make one click to conduct several descriptive statistical analyses. Among them are the following.
Rice Virtual Lab in Statistics
http://onlinestatbook.com/stat_analysis/index.html
VassarStats
http://faculty.vassar.edu/lowry/VassarStats.html
Bright Stat
For a more complete list, see http://statpages.org/index.html.
KEY TAKEAWAYS
- Every variable has a distribution—a way that the scores are distributed across the levels. The distribution can be described using a frequency table and histogram. It can also be described in words in terms of its shape, including whether it is unimodal or bimodal, and whether it is symmetrical or skewed.
- The central tendency, or middle, of a distribution can be described precisely using three statistics—the mean, median, and mode. The mean is the sum of the scores divided by the number of scores, the median is the middle score, and the mode is the most common score.
- The variability, or spread, of a distribution can be described precisely using the range and standard deviation. The range is the difference between the highest and lowest scores, and the standard deviation is roughly the average amount by which the scores differ from the mean.
- The location of a score within its distribution can be described using percentile ranks or z scores. The percentile rank of a score is the percentage of scores below that score, and the zscore is the difference between the score and the mean divided by the standard deviation.
EXERCISES
- Practice: Make a frequency table and histogram for the following data. Then write a short description of the shape of the distribution in words.
11, 8, 9, 12, 9, 10, 12, 13, 11, 13, 12, 6, 10, 17, 13, 11, 12, 12, 14, 14 - Practice: For the data in Exercise 1, compute the mean, median, mode, standard deviation, and range.
- Practice: Using the data in Exercises 1 and 2, find (a) the percentile ranks for scores of 9 and 14 and (b) the z scores for scores of 8 and 12.
- 7537 reads






