Imagine that a health psychologist is interested in the accuracy of college students’ estimates of the number of calories in a chocolate chip cookie. He shows the cookie to a sample of 10
students and asks each one to estimate the number of calories in it. Because the actual number of calories in the cookie is 250, this is the hypothetical population mean of interest (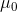 ). The null hypothesis is that the mean estimate for the population (μ) is
250. Because he has no real sense of whether the students will underestimate or overestimate the number of calories, he decides to do a two-tailed test. Now imagine further that the
participants’ actual estimates are as follows:
). The null hypothesis is that the mean estimate for the population (μ) is
250. Because he has no real sense of whether the students will underestimate or overestimate the number of calories, he decides to do a two-tailed test. Now imagine further that the
participants’ actual estimates are as follows:
250, 280, 200, 150, 175, 200, 200, 220, 180, 250.
The mean estimate for the sample (M) is 212.00 calories and the standard deviation (SD) is 39.17. The health psychologist can now compute the t score for his sample:
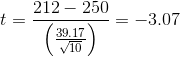
If he enters the data into one of the online analysis tools or uses SPSS, it would also tell him that the two- tailed p value for this tscore (with 10 − 1 = 9 degrees of freedom) is .013. Because this is less than .05, the health psychologist would reject the null hypothesis and conclude that college students tend to underestimate the number of calories in a chocolate chip cookie. If he computes the t score by hand, he could look at Table 13.2 and see that the critical value of tfor a two-tailed test with 9 degrees of freedom is ±2.262. The fact that his t score was more extreme than this critical value would tell him that his p value is less than .05 and that he should reject the null hypothesis.
Finally, if this researcher had gone into this study with good reason to expect that college students underestimate the number of calories, then he could have done a one-tailed test instead of a two-tailed test. The only thing this would change is the critical value, which would be −1.833. This slightly less extreme value would make it a bit easier to reject the null hypothesis. However, if it turned out that college students overestimate the number of calories—no matter how much they overestimate it—the researcher would not have been able to reject the null hypothesis.
- 1921 reads






