Example One-Way ANOVA

Available under Creative Commons-NonCommercial-ShareAlike 4.0 International License.

Imagine that the health psychologist wants to compare the calorie estimates of psychology majors, nutrition majors, and professional dieticians. He collects the following data:

Psych majors: 200, 180, 220, 160, 150, 200, 190, 200 Nutrition majors: 190, 220, 200, 230, 160, 150, 200, 210, 195Dieticians: 220, 250, 240, 275, 250, 230, 200, 240

The means are 187.50 (SD= 23.14), 195.00 (SD= 27.77), and 238.13 (SD= 22.35), respectively. So it appears that dieticians made substantially more accurate estimates on average. The researcher would almost certainly enter these data into a program such as Excel or SPSS, which would compute F for him and find the p value. Table 13.4 shows the output of the one-way ANOVA function in Excel for these data. This is referred to as an ANOVA table. It shows that MSB is 5,971.88, MSW is 602.23, and their ratio, F, is 9.92. The p value is .0009. Because this is below .05, the researcher would reject the null hypothesis and conclude that the mean calorie estimates for the three groups are not the same in the population. Notice that the ANOVA table also includes the “sum of squares” (SS) for between groups and for within groups. These values are computed on the way to finding MSB and MSW but are not typically reported by the researcher. Finally, if the researcher were to compute the F ratio by hand, he could look at Table 13.3 and see that the critical value of F with 2 and 21 degrees of freedom is 3.467 (the same value in Table 13.4 under 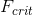). The fact that his t score was more extreme than this critical value would tell him that his p value is less than .05 and that he should reject the null hypothesis.