A common characteristic in the pricing of many goods is that different individuals pay different prices for goods or services that are essentially the same. Examples abound: Seniors get a reduced rate for coffee in Burger King; hair salons charge women more than they charge men; bank charges are frequently waived for juniors. Price discrimination involves charging different prices to different consumers in order to increase profit.
 Price discrimination involves charging different
prices to different consumers in order to increase profit.
Price discrimination involves charging different
prices to different consumers in order to increase profit.
A strict definition of discrimination involves different prices for identical products. We all know of a school friend who has been willing to take the midnight flight to make it home at school break at a price he can afford. In contrast, the business executive prefers the seven a.m. flight to arrive for a nine a.m. business meeting in the same city at several times the price. These are very mild forms of price discrimination, since a midnight flight (or a mid-day flight) is not a perfect substitute for an early morning flight. Price discrimination is practiced because buyers are willing to pay different amounts for a good or service, and the supplier may have a means of profiting from this. Consider the following example.
Family Flicks is the local movie theatre. It has two distinct groups of customers – those of prime age form one group; youth and seniors form the other. Family Flicks has done its market research and determined that each group accounts for 50 percent of the total market of 100 potential viewers per screening. It has also established that the prime-age group members are willing to pay $12 to see a movie, while the seniors and youth are willing to pay just $5. How should the tickets be priced?
Family Flicks has no variable costs, only fixed costs. It must pay a $100 royalty to the movie maker each time it shows the current movie, and must pay a cashier and usher $20 each. Total costs are therefore $140, regardless of how many people show up – short-run MC is zero. On the pricing front, as illustrated in Table 10.2 below, if Family Flicks charges $12 per ticket it will attract 50 viewers, generate $600 in revenue and therefore make a profit of $460.
| P=$5 | P=$12 | Twin price | |
| No. of customers | 100 | 50 | |
| Total revenue | $500 | $600 | $850 |
| Total costs | $140 | $140 | $140 |
| Profit | $360 | $460 | $710 |
In contrast, if it charges $5 it can fill the theatre, because each of the prime-age individuals is willing to pay more than $5, but the seniors and youth are now offered a price they too are willing to pay. However, the total revenue is now only $500 (100X$5 = $500), and profits are reduced to $360. It therefore decides to charge the high price and leave the theatre half-empty, because this strategy maximizes its profit.
Suppose finally that the theatre is able to segregate its customers. It can ask the young and senior customers for identification upon entry, and in this way charge them a lower price, while still maintaining the higher price to the prime-age customers. If it can execute such a plan Family Flicks can now generate $850 in revenue – $600 from the prime-age group and $250 from the youth and seniors groups. Profit soars to $710.
There are two important conditions for this scheme to work:
- The seller must be able to segregate the market at a reasonable cost. In the movie case this is achieved by asking for identification.
- The second condition is that resale must be impossible or impractical. For example, we rule out the opportunity for young buyers to resell their tickets to the prime-age individuals.
Sellers have many ways of achieving this – they can require immediate entry to the movie theatre upon ticket purchase, they can stamp the customer’s hand, they can demand the showing of ID with the ticket when entering the theatre area.
Frequently we think of sellers who offer price reductions to specific groups as being generous. For example, hotels may levy only a nominal fee for the presence of a child, once the parents have paid a suitable rate for the room or suite in which a family stays. The hotel knows that if it charges too much for the child, it may lose the whole family as a paying unit. The coffee shop offering cheap coffee to seniors is interested in getting a price that will cover its variable cost and so contribute to its profit. It is unlikely to be motivated by philanthropy, or to be concerned with the financial circumstances of seniors.
Price discrimination has a further interesting feature that is illustrated in Figure 10.10: it frequently reduces the deadweight loss associated with a monopoly seller!
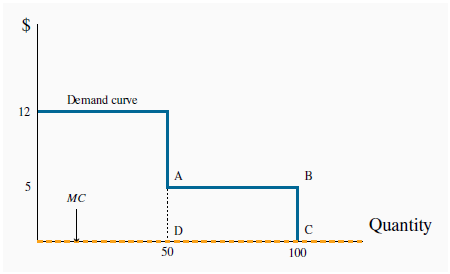
At P = 12, 50 prime-age individuals demand movie tickets. At P = 5, 50 more seniors and youths demand tickets. Since the MC is zero the efficient output is where the demand curve takes a zero value – where all 100 customers purchase tickets. Thus, any scheme that results in all 100 individuals buying ticket is efficient. Efficient output is at point C.
In our Family Flicks example, the profit maximizing monopolist that did not, or could not, price discriminate left 50 customers unsupplied who were willing to pay $5 for a good that had a zero MC. This is a deadweight loss of $250 because 50 seniors and youth valued a commodity at $5 that had a zero MC. Their demand was not met because, in the absence of an ability to discriminate between consumer groups, Family Flicks made more profit by satisfying the demand of the prime-age group. But in this example, by segregating its customers, the firm’s profit maximization behaviour resulted in the DWL being eliminated, because it supplied the product to those additional 50 individuals. In this instance price discrimination improves welfare, because more of a good is supplied in a situation where market valuation exceeds marginal cost.
In the preceding example we simplified the demand side of the market by assuming that every individual in a given group was willing to pay the same price – either $12 or $5. More realistically each group can be defined by a downward-sloping demand curve, reflecting the variety of prices that buyers in a given market segment are willing to pay. It is valuable to extend the analysis to include this reality. For example, a supplier may face different demands from her domestic and foreign buyers, and if she can segment these markets she can price discriminate effectively.
Consider Figure 10.11 where two segmented demands are displayed, DA and DB, with their associated marginal revenue curves, MRA and MRB. We will assume that marginal costs are constant for the moment. It should be clear by this point that the profit maximizing solution for the monopoly supplier is to supply an amount to each market where the MC equals the MR in each market: since the buyers in one market cannot resell to buyers in the other, the monopolist considers these as two different markets and therefore maximizes profit by applying the standard rule. She will maximize profit in market A by supplying the quantity QA and in market B by supplying QB. The prices at which these quantities can be sold are PA and PB. These prices, unsurprisingly, are different – the objective of segmenting markets is to increase profit by treating the markets as distinct.
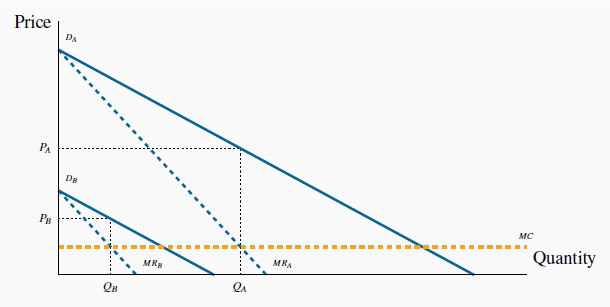
With two separate markets defined by 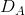 and
and 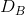 , and their associated MR curves MRA and MRB, a profit maximizing strategy is to produce
where MC =
, and their associated MR curves MRA and MRB, a profit maximizing strategy is to produce
where MC = 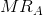 =
= 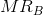 , and discriminate between the two markets by charging prices
, and discriminate between the two markets by charging prices 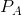 and
and 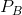 .
.
The preceding examples involved two separable groups of customers and are very real. This kind of group segregation is sometimes called third degree price discrimination. But it may be possible to segregate customers into several groups rather than just two. In the limit, if we could charge a different price to every consumer in a market, or for every unit sold, the revenue accruing to the monopolist would be the area under the demand curve up to the output sold. Though primarily of theoretical interest, this is illustrated in Figure 10.12. It is termed perfect price discrimination, and sometimes first degree price discrimination. Such discrimination is not so unrealistic: a tax accountant may charge different customers a different price for providing the same service; home renovators may try to charge as much as any client appears willing to pay.
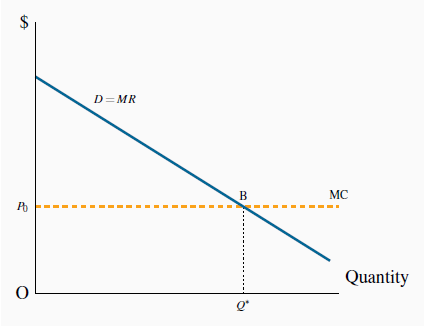
A monopolist who can sell each unit at a different price maximizes profit by producing Q*. With each consumer paying a different price the demand curve becomes the MR curve. The result is that the monopoly DWL is eliminated because the efficient output is produced, and the monopolist appropriates all the consumer surplus. Total revenue for the perfect price discriminator is OABQ*.
Second degree price discrimination is based on a different concept of buyer identifiability. In the cases we have developed above, the seller is able to distinguish the buyers by observing a vital characteristic that signals their type. But it is also possible that, while individuals might have defining traits which influence their demands, such traits might not be detectable by the supplier. Nonetheless, it may be possible for her to offer different pricing options that buyers would choose from, with the result that her profit would be greater than under a uniform price. Different cell phone ‘plans’ or different internet plans that users can choose from are an example of this second degree discrimination.
- 2717 reads






