As long as design requirements are met, the input-output relation for the inverting amplifier also applies when the feedback and input circuit elements are impedances (resistors, capacitors, and inductors).
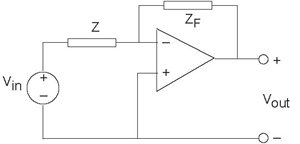
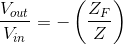
Example 3.7
Let's design an op-amp circuit that functions as a lowpass filter. We want the transfer function between the output and input voltage to be
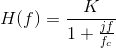
where K equals the passband gain and fc is the cutoff frequency. Let's
assume that the inversion (negative gain) does not matter. With the transfer function of the above op-amp circuit in mind, let's consider some choices.
-
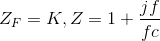 . This choice means the feedback impedance is a resistor and
that the input impedance is a series combination of an inductor and a resistor. In circuit design, we try to avoid inductors because they are physically bulkier than capacitors.
. This choice means the feedback impedance is a resistor and
that the input impedance is a series combination of an inductor and a resistor. In circuit design, we try to avoid inductors because they are physically bulkier than capacitors.
-
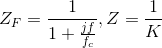 . Consider the reciprocal of the
feedback impedance (its admittance):
. Consider the reciprocal of the
feedback impedance (its admittance):
-
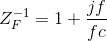 . Since this admittance is a sum of admittances, this
expression suggests the parallel combination of a resistor (value 1 Ω) and a capacitor (value
. Since this admittance is a sum of admittances, this
expression suggests the parallel combination of a resistor (value 1 Ω) and a capacitor (value 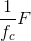 ). We have the right idea, but the values (like 1 Ω) are not right. Consider the general RC parallel combination: its admittance is
). We have the right idea, but the values (like 1 Ω) are not right. Consider the general RC parallel combination: its admittance is 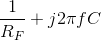 . Letting the input resistance equal R, the transfer function of the op-amp inverting
amplifier now is
. Letting the input resistance equal R, the transfer function of the op-amp inverting
amplifier now is 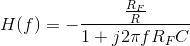
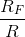 and the cutoff frequency
and the cutoff frequency 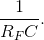
Creating a specific transfer function with op-amps does not have a unique answer. As opposed to design with passive circuits, electronics is more flexible (a cascade of circuits can be built so
that each has little effect on the others; see Problem 3.44) and gain (increase in power and amplitude) can result. To complete our example, let's assume we want a lowpass filter that emulates
what the telephone companies do. Signals transmitted over the telephone have an upper frequency limit of about 3 kHz. For the second design choice, we require RF C =3.3×10−4 . Thus, many choices for
resistance and capacitance values are possible. A 1 µF capacitor and a 330 Ω resistor, 10 nF and 33 kΩ, and 10 pF and 33 MΩ would all theoretically work. Let's also desire a voltage gain of
ten: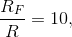 which means
which means 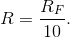 Recall that we must have R<Rin. As the op-amp's input impedance is about 1 MΩ, we don't want R too large, and this requirement means that the last choice for resistor/capacitor values
won't work. We also need to ask for less gain than the op-amp can provide itself. Because the feedback "element" is an impedance (a parallel resistor capacitor combination), we need to examine
the gain requirement more carefully. We must have
Recall that we must have R<Rin. As the op-amp's input impedance is about 1 MΩ, we don't want R too large, and this requirement means that the last choice for resistor/capacitor values
won't work. We also need to ask for less gain than the op-amp can provide itself. Because the feedback "element" is an impedance (a parallel resistor capacitor combination), we need to examine
the gain requirement more carefully. We must have 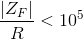 for all
frequencies of interest. Thus,
for all
frequencies of interest. Thus, 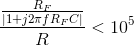 . As
this impedance decreases with frequency, the design specification of
. As
this impedance decreases with frequency, the design specification of 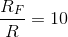 means that this criterion is easily met. Thus, the first two choices for the resistor and capacitor values (as well as many others in this range) will work well. Additional considerations like
parts cost might enter into the picture. Unless you have a high-power application (this isn't one) or ask for high-precision components, costs don't depend heavily on component values as long
as you stay close to standard values. For resistors, having values r10d, easily obtained values of r are 1, 1.4, 3.3, 4.7,
and 6.8, and the decades span 0-8.
means that this criterion is easily met. Thus, the first two choices for the resistor and capacitor values (as well as many others in this range) will work well. Additional considerations like
parts cost might enter into the picture. Unless you have a high-power application (this isn't one) or ask for high-precision components, costs don't depend heavily on component values as long
as you stay close to standard values. For resistors, having values r10d, easily obtained values of r are 1, 1.4, 3.3, 4.7,
and 6.8, and the decades span 0-8.
Exercise 3.19.1
What is special about the resistor values; why these rather odd-appearing values for r?
- 3204 reads






