The information contained in the spoken word is conveyed by the speech signal. Because we shall analyze several speech transmission and processing schemes, we need to understand the speech signal's structure what's special about the speech signal and how we can describe and model speech production. This modeling effort consists of finding a system's description of how relatively unstructured signals, arising from simple sources, are given structure by passing them through an interconnection of systems to yield speech. For speech and for many other situations, system choice is governed by the physics underlying the actual production process. Because the fundamental equation of acoustics the wave equation applies here and is linear, we can use linear systems in our model with a fair amount of accuracy. The naturalness of linear system models for speech does not extend to other situations. In many cases, the underlying mathematics governed by the physics, biology, and/or chemistry of the problem are nonlinear, leaving linear systems models as approximations. Nonlinear models are far more difcult at the current state of knowledge to understand, and information engineers frequently prefer linear models because they provide a greater level of comfort, but not necessarily a sufcient level of accuracy.
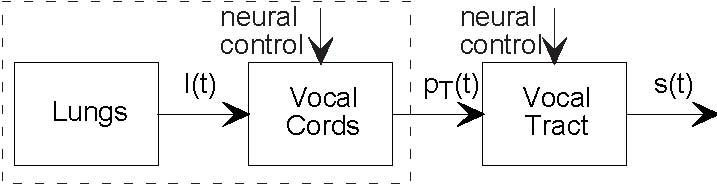
Figure 4.13 shows the actual speech production system and Figure 4.14 shows the model speech production system. The characteristics of the model depends on whether you are saying a vowel or a consonant. We concentrate first on the vowel production mechanism. When the vocal cords are placed under tension by the surrounding musculature, air pressure from the lungs causes the vocal cords to vibrate. To visualize this efect, take a rubber band and hold it in front of your lips. If held open when you blow through it, the air passes through more or less freely; this situation corresponds to "breathing mode". If held tautly and close together, blowing through the opening causes the sides of the rubber band to vibrate. This effect works best with a wide rubber band. You can imagine what the airflow is like on the opposite side of the rubber band or the vocal cords. Your lung power is the simple source referred to earlier; it can be modeled as a constant supply of air pressure. The vocal cords respond to this input by vibrating, which means the output of this system is some periodic function.
Exercise 4.10.1
Note that the vocal cord system takes a constant input and produces a periodic airflow that corresponds to its output signal. Is this system linear or nonlinear? Justify your answer.
Singers modify vocal cord tension to change the pitch to produce the desired musical note. Vocal cord tension is governed by a control input to the musculature; in system's models we represent control inputs as signals coming into the top or bottom of the system. Certainly in the case of speech and in many other cases as well, it is the control input that carries information, impressing it on the system's output. The change of signal structure resulting from varying the control input enables information to be conveyed by the signal, a process generically known as modulation. In singing, musicality is largely conveyed by pitch; in western speech, pitch is much less important. A sentence can be read in a monotone fashion without completely destroying the information expressed by the sentence. However, the difference between a statement and a question is frequently expressed by pitch changes. For example, note the sound differences between "Let's go to the park." and "Let's go to the park?";
For some consonants, the vocal cords vibrate just as in vowels. For example, the so-called nasal sounds "n" and "m" have this property. For others, the vocal cords do not produce a periodic output. Going back to mechanism, when consonants such as "f" are produced, the vocal cords are placed under much less tension, which results in turbulent flow. The resulting output airflow is quite erratic, so much so that we describe it as being noise. We define noise carefully later when we delve into communication problems.
The vocal cords' periodic output can be well described by the periodic pulse train pT (t) as shown in the periodic pulse signal (Figure 4.1), with T denoting the pitch period. The spectrum of this signal (4.9) contains harmonics of the frequency 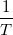 , what is known as the pitch frequency or the
fundamental frequency F0. The primary difference between adult male and female/prepubescent speech is pitch. Before puberty, pitch frequency for normal speech
ranges between 150-400 Hz for both males and females. After puberty, the vocal cords of males undergo a physical change, which has the effect of lowering their pitch frequency to the range
80-160 Hz. If we could examine the vocal cord output, we could probably discern whether the speaker was male or female. This diference is also readily apparent in the speech signal itself.
, what is known as the pitch frequency or the
fundamental frequency F0. The primary difference between adult male and female/prepubescent speech is pitch. Before puberty, pitch frequency for normal speech
ranges between 150-400 Hz for both males and females. After puberty, the vocal cords of males undergo a physical change, which has the effect of lowering their pitch frequency to the range
80-160 Hz. If we could examine the vocal cord output, we could probably discern whether the speaker was male or female. This diference is also readily apparent in the speech signal itself.
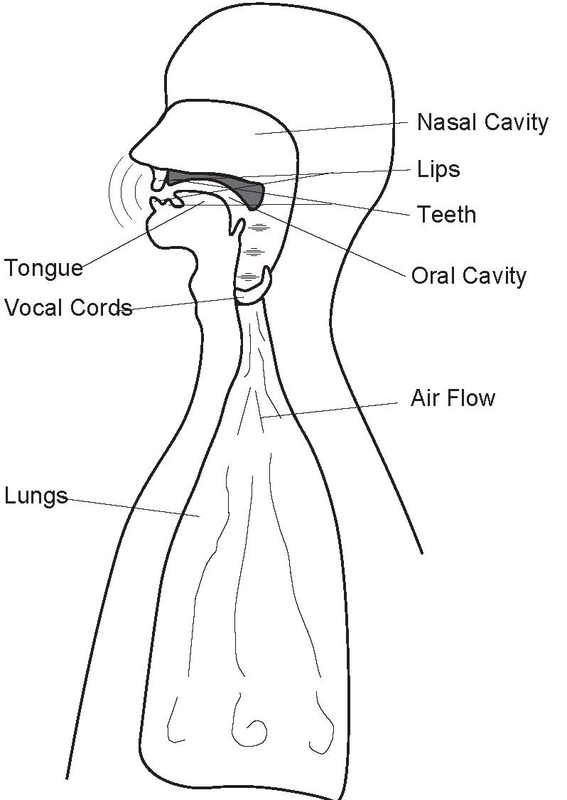
To simplify our speech modeling efort, we shall assume that the pitch period is constant. With this simplifcation, we collapse the vocal-cord-lung system as a simple source that produces the periodic pulse signal (Figure 4.14). The sound pressure signal thus produced enters the mouth behind the tongue, creates acoustic disturbances, and exits primarily through the lips and to some extent through the nose. Speech specialists tend to name the mouth, tongue, teeth, lips, and nasal cavity the vocal tract. The physics governing the sound disturbances produced in the vocal tract and those of an organ pipe are quite similar. Whereas the organ pipe has the simple physical structure of a straight tube, the cross-section of the vocal tract "tube" varies along its length because of the positions of the tongue, teeth, and lips. It is these positions that are controlled by the brain to produce the vowel sounds. Spreading the lips, bringing the teeth together, and bringing the tongue toward the front portion of the roof of the mouth produces the sound "ee." Rounding the lips, spreading the teeth, and positioning the tongue toward the back of the oral cavity produces the sound "oh." These variations result in a linear, time-invariant system that has a frequency response typifed by several peaks, as shown in Figure 4.15.
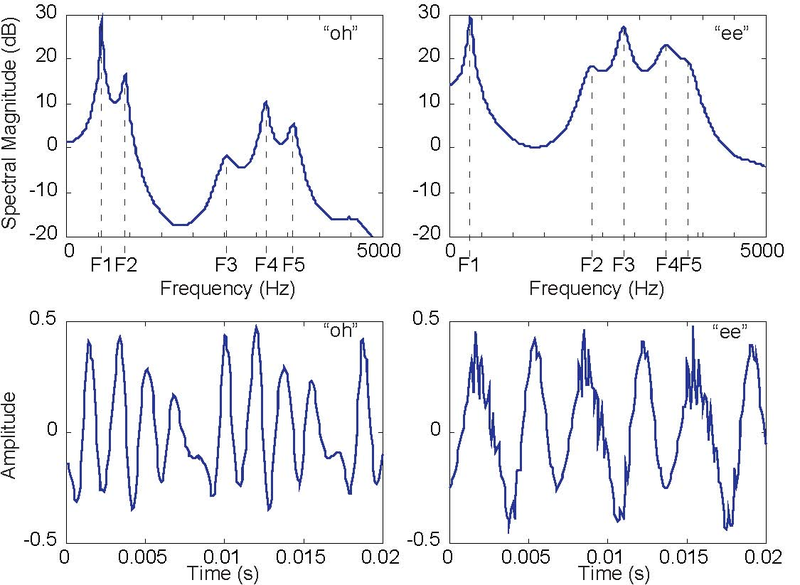
These peaks are known as formants. Thus, speech signal processors would say that the sound "oh" has a higher first formant frequency than the sound "ee," with F2 being much higher during "ee." F2 and F3 (the second and third formants) have more energy in "ee" than in "oh." Rather than serving as a filter, rejecting high or low frequencies, the vocal tract serves to shape the spectrum of the vocal cords. In the time domain, we have a periodic signal, the pitch, serving as the input to a linear system. We know that the output the speech signal we utter and that is heard by others and ourselves will also be periodic. Example time-domain speech signals are shown in Figure 4.15, where the periodicity is quite apparent.
Exercise 4.10.2
From the waveform plots shown in Figure 4.15, determine the pitch period and the pitch frequency. Since speech signals are periodic, speech has a Fourier series representation given by a linear circuit's response to a periodic signal (4.27). Because the acoustics of the vocal tract are linear, we know that the spectrum of the output equals the product of the pitch signal's spectrum and the vocal tract's frequency response. We thus obtain the fundamental model of speech production.
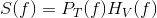
Here, HV (f) is the transfer function of the vocal tract system. The Fourier series for the vocal cords' output, derived in this equation (p. 122), is
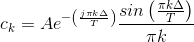
and is plotted on the top in Figure 4.16. If we had, for example, a male
speaker with about a 110 Hz pitch (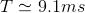 ) saying the vowel "oh", the spectrum of
his speech predicted by our model is shown in Figure 4.16.
) saying the vowel "oh", the spectrum of
his speech predicted by our model is shown in Figure 4.16.
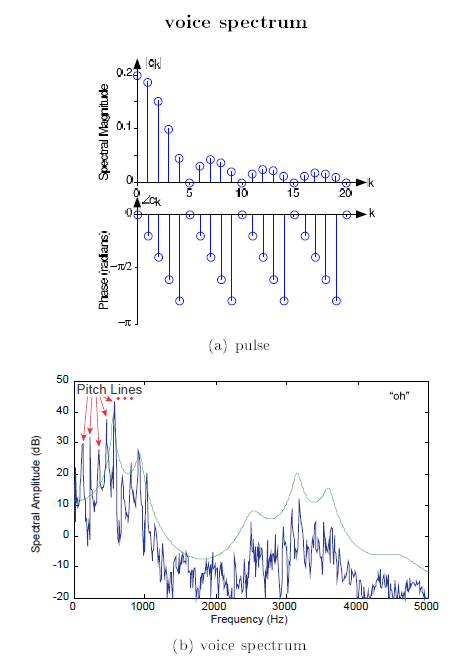
The model spectrum idealizes the measured spectrum, and captures all the important features. The measured spectrum certainly demonstrates what are known as pitch lines, and we realize from our model that they are due to the vocal cord's periodic excitation of the vocal tract. The vocal tract's shaping of the line spectrum is clearly evident, but difficult to discern exactly, especially at the higher frequencies. The model transfer function for the vocal tract makes the formants much more readily evident.
Exercise 4.10.3
The Fourier series coefficients for speech are related to the vocal tract's transfer function only at the frequencies 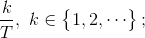 see previous result (4.9). Would male or female speech tend to
see previous result (4.9). Would male or female speech tend to
T have a more clearly identifiable formant structure when its spectrum is computed? Consider, for example, how the spectrum shown on the right in Figure 4.16 would change if the pitch were twice as high (≈ (300) Hz).
When we speak, pitch and the vocal tract's transfer function are not static; they change according to their control signals to produce speech. Engineers typically display how the speech spectrum changes over time with what is known as a Spectrograms Figure 4.17. Note how the line spectrum, which indicates how the pitch changes, is visible during the vowels, but not during the consonants (like the ce in "Rice").
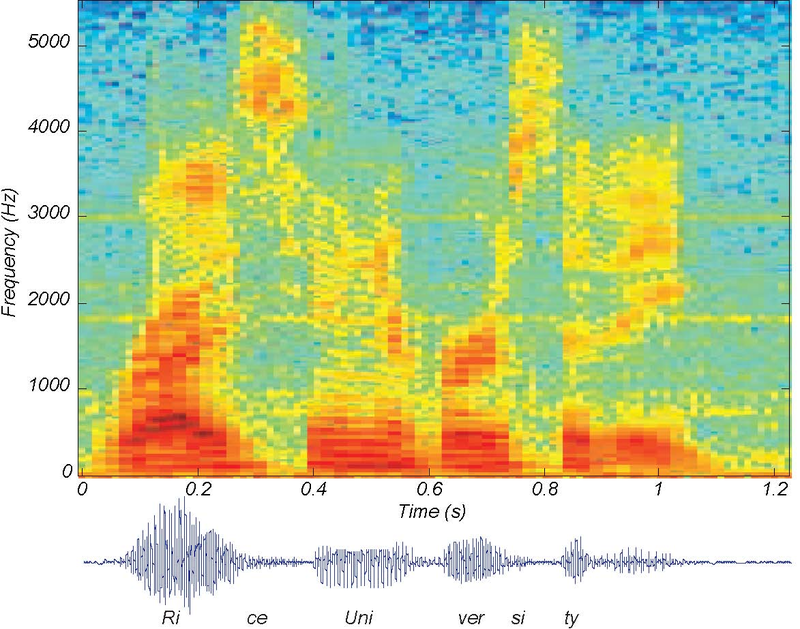
The fundamental model for speech indicates how engineers use the physics underlying the signal generation process and exploit its structure to produce a systems model that suppresses the physics while emphasizing how the signal is "constructed." From everyday life, we know that speech contains a wealth of information. We want to determine how to transmit and receive it. Efficient and effective speech transmission requires us to know the signal's properties and its structure (as expressed by the fundamental model of speech production). We see from Figure 4.17, for example, that speech contains significant energy from zero frequency up to around 5 kHz.
Effective speech transmission systems must be able to cope with signals having this bandwidth. It is interesting that one system that does not support this 5 kHz bandwidth is the telephone: Telephone systems act like a bandpass filter passing energy between about 200 Hz and 3.2 kHz. The most important consequence of this filtering is the removal of high frequency energy. In our sample utterance, the "ce" sound in "Rice"" contains most of its energy above 3.2 kHz; this filtering effect is why it is extremely difficult to distinguish the sounds "s" and "f" over the telephone. Try this yourself: Call a friend and determine if they can distinguish between the words "six" and "fx". If you say these words in isolation so that no context provides a hint about which word you are saying, your friend will not be able to tell them apart. Radio does support this bandwidth (see more about Signal-to-Noise Ratio of an Amplitude-Modulated Signal ).
Efficient speech transmission systems exploit the speech signal's special structure: What makes speech speech? You can conjure many signals that span the same frequencies as speech car engine sounds, violin music, dog barks but don't sound at all like speech. We shall learn later that transmission of any 5 kHz bandwidth signal requires about 80 kbps (thousands of bits per second) to transmit digitally. Speech signals can be transmitted using less than 1 kbps because of its special structure. To reduce the "digital bandwidth" so drastically means that engineers spent many years to develop signal processing and coding methods that could capture the special characteristics of speech without destroying how it sounds. If you used a speech transmission system to send a violin sound, it would arrive horribly distorted; speech transmitted the same way would sound fine.
Exploiting the special structure of speech requires going beyond the capabilities of analog signal processing systems. Many speech transmission systems work by finding the speaker's pitch and the formant frequencies. Fundamentally, we need to do more than filtering to determine the speech signal's structure; we need to manipulate signals in more ways than are possible with analog systems. Such flexibility is achievable (but not without some loss) with programmable digital systems.
- 6121 reads






