了解各种效度与信度之后,让我来用数学表示的方法(经典检验理论或真值理论)对信度与效度的相关理解进行综合。这是一个用来研究测量是如何工作的,其测量了什么以及没有测量什么的一个心理测量理论。该理论假设每次观测有一个真实值T,这个真实值可以在没有测量误差的情况下精确观测得到,然而,观测过程通常会存在误差E,这些误差的存在使得观测值X与真实值T之间存在偏离。
| X | = | T | + | E |
| 观测值 | 真实值 | 误差 |
根据观测结果,观测值与真实值方差的关系可以用相似的公式来表达:
var(X)=var(T)+var(E)
心理测量分析的目标是估计并尽可能地减小var(E),这样观测值X可作为真实值T的一个好的测量。
测量误差分为两种类型:随机误差和系统误差。随机误差是指由不可预知和不可控制的偶发外部因素所引起的误差。比如,在测量过程中,一些被试的情绪状态可能比其他被试好一些,这将会影响被试对测量项目的反应,情绪好的被试对自尊、满意度以及幸福指数等构念项目的反应可能比情绪状态差的人积极,然而,预测或者控制被试的情绪状态是不可能的;
同理,在进行组织层面的测量时,如测量企业绩效,制度和环境变化可能会影响观测样本中的一些企业,而其他的企业则不受影响,因此,随机误差被视为测量中的“噪音”,通常忽略不计。
系统误差是指由系统整体因素所引起的,影响样本中所有个体观测值所形成的普遍误差。接我们前面的例子,相比于制造业或者服务业企业,金融危机更多的影响了金融企业的绩效,假设样本只包含金融企业,我们预期金融危机给样本带来了普遍性的绩效下降。随机误差可能是正向、负向或者是零,然而系统误差则会表现为样本中所有个体观测值的同向变化(正向或者负向),因此,系统误差通常被认为是偏差,且需要得到修正。
由于观测值可能包含随机误差和系统误差,可将上述的真实值等式修正如下:
X=T+Er+Es
Er、Es分别代表随机误差和系统误差,随机误差会对观测值分布的差异性指标(如方差)产生影响,不会影响居中趋势;而系统误差则会影响居中趋势(如均值),不会影响差异性指标(如图表 7.5所示):
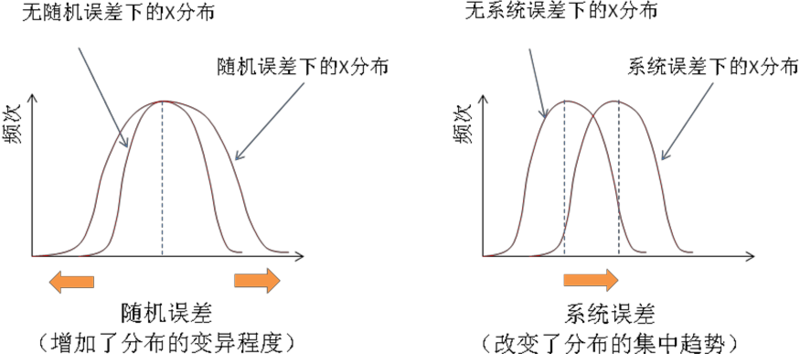
随机误差和系统误差对测量过程意味着什么呢?随机误差通过增加观测值的变异程度使得测量的信度降低,相反地,系统误差通过影响居中趋势降低测量的效度。
在测量中,效度通常比信度更重要,这是由于低效度的测量意味着可能测量的并不是我们试图测量的构念,因此,效度对基于数据分析的研究特别关键。
由于信度是真实值与观测值之间的比例关系,因此,信度可以由下式表示:
var(T)/var(X)=var(T)/[var(T)+var(E)]
如果真实值与观测值的方差相等,那么信度为1。
- 5505 reads






