准实验设计几乎与真实验设计完全相同,除了一个方面不同:随机分派。例如,整个班级或组织被当做实验组而另一个班级或同一个行业内的另一个组织被当做控制组。由于缺乏随机分派,这些组并不等价,例如一个组比另一个组在某些内容上更优越(比如说在上学期有更好的老师),这将有可能导致选样偏差。准实验设计在内部效度上不如真实验设计,因为其存在各种各样的选样相关威胁如选样成熟度威胁(实验组与控制组具有不同的成熟水平),选样历史威胁(实验组与控制组受随机因素或历史事件的影响不同),选样回归威胁(实验组与控制组对前测后测均值的回归比例不同),选样测量威胁(实验组与控制组对测量的反应不同),选样测试威胁(实验组与控制组对前测的反应不同),选样流失威胁(实验组与控制组的样本流失率不同)。鉴于这么多的选样威胁,一般尽可能地避免采用准实验设计。
许多真实验设计可以在忽略随机分派时被转化为准实验设计。例如,前测-后测控制组设计的准实验版本被称作不等对照组设计,如图表 10.8所示,随机分派R被替换为不等(非随机)分派N。同样,切换重复设计的准实验版本被称作不等切换重复设计(见图表 10.9)。
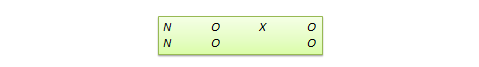
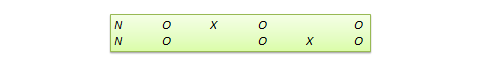
此外,很少有那种真实验设计没有其对应的准实验版本。下面将讨论其他一些有用的设计。
界断点回归设计。这是一种不等前测-后测设计,根据事前某一测量的界点值将被试分派到实验组与控制组中。例如,重症病人被分到实验组以检测某种新药或处理方式的有效性,那些病情轻微的病人被分派到控制组中。另一个例子,那些落后于标准考试成绩的学生被选入课程补习班以提高他们的成绩,而不将那些考试成绩优异的学生选入补习班。这种设计可以用下图来标注,其中C代表界点值。
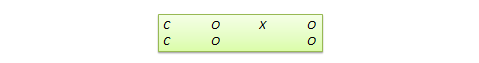
因为采用了界点值,观测结果很可能是由于界点值本身影响的而非实验处理影响的,这将威胁到内部效度。尽管如此,采用界点值也促使将有限的资源分配给那些最需要这些资源的人而非随机进行分配,同时这也可以作为一种准实验的实验处理。在界断点回归设计中,考虑两组之间的系统性的不等价性,控制组的成绩并不作为与实验组进行比较的标杆。如果在控制组中的前测与后测并不存在不连续性,而这种不连续性出现在了实验组,那么这种不连续性可视作实验处理的影响的证据。
代理前测设计。如图表 10.11所示,这种设计与标准的不等对照组设计(前测-后测)非常相像,区别在于前测值是在执行实验处理之后收集的。这种设计的一种典型应用情景是:研究者想要检验某个项目(如一个教育项目)的有效性,然后该项目已经实施使得前测数据无法获取。在这种情况下,研究者的最好选择是利用一个提前记录的一个测量,例如学生在项目开始时的平均积分点作为前测的代理数据。代理前测设计的一种变化形式是在被试进行后测时对前测数据进行重新收集,不过这种方法具有回忆偏倚的风险,但不管如何,这也是提供了一种对因变量的感知收益或变化的测量。
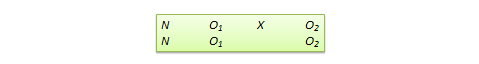
个别样本的前后测设计。当基于同一种原因从同一个样本收集前测与后测数据不太可能时,这种设计方法非常适用。如图表 10.12所示,该设计有四个组,其中两个组来自同一个不对等组,而另两个组来自不同的不对等组。例如,你要检验客户对于某种在一个城市予以实施但在另一城市没有实施的新的在线服务的满意度,那么在第一个城市的客户可以作为实验组,而另一个城市的客户作为控制组。如果不可能从同一批客户中获得前测与后测的数据,你可以在某个时间点测量客户满意度,实施新服务项目,然后测量项目实施后的客户满意度(此时的客户与前测时的客户不同)。在同一时间点对控制组的客户满意度进行测量,不过该组并没有实施新项目。这种设计并不非常严谨,因为你不能测量特定客户在新项目实施前后满意度分值的变化,你只能检验客户满意度的平均值。尽管该设计内部效度较低,其仍然是在前后测数据无法从同一被试获取的情况下的一种非常有用的准实验数据收集方法。

非对等因变量设计。这是针对同一组群的前后测准实验设计,具有两个结果测量,其中一个测量从理论上应该受到实验处理的影响而另一个测量并不受此影响。例如,如果你要为高中生设计一个新的微积分课程,该课程将很可能影响微积分成绩而不会影响代数成绩。尽管如此,在后测时代数成绩也可能会因为随机因素(如历史或成熟性因素)而有所变化。因此,前后测的代数成绩可以用作一种控制测量,而前后测的微积分成绩则被视作实验测量。该设计标注可以用图表 10.13来表示,N表示单组,O1和O2表示同一组学生在前后测中的微积分与代数学成绩。该设计在内部效度上存在不足,但其优势在于不需要一个独立的控制组。
非对等因变量设计的一种变化形式被称作模式匹配的非对等因变量设计。这种设计采用多个结果变量并采用一个理论来解释这些变量将如何受到实验处理的影响,然后研究者可以检测理论预测值是否与实际观测值所匹配。这种基于理论模式与观测模式的对应程度的模式匹配技术可以有效地消除原始的非对等因变量设计的内部效度问题。
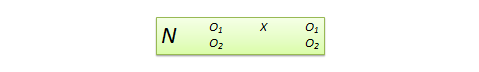
- 15528 reads






