Toward the end of the eighteenth century, a German elementary school teacher decided to keep his pupils busy by assigning them a long, boring arithmetic problem: to add up all the numbers from one to a hundred. 1 The children set to work on their slates, and the teacher lit his pipe, confident of a long break. But almost immediately, a boy named Carl Friedrich Gauss brought up his answer: 5,050.
Figure 1.1 suggests one way of solving this type of problem. The filled-in columns of the graph represent the numbers from 1 to 7, and adding them up means finding the area of the shaded region.
Roughly half the square is shaded in, so if we want only an approximate solution, we can simply calculate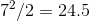 
.
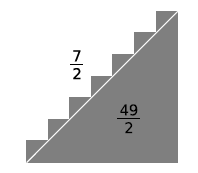
But, as suggested in Figure 1.2, it's not much more
work to get an exact result. There are seven sawteeth sticking out out above the diagonal, with a total area of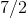 
, so the total shaded area is 
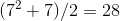. In general, the sum of the first 
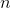numbers will be
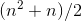, which explains Gauss's result: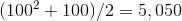 
- 瀏覽次數：2203
