We can differentiate any function that is written as a formula, and find a result in terms of a formula. However, sometimes the original problem can’t be written in any nice way as a formula. For example, suppose we want to find dy/ dx in a case where the relationship be- tween x and y is given by the following equation:
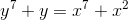
There is no equivalent of the quadratic formula for seventh- order polynomials, so we have no way to solve for one variable in terms of the other in order to differentiate it. However, we can
still find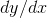 
in terms of 
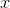and 
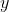. Suppose we let 
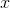grow to 
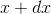. Then for example the 
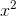term will grow to 
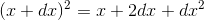. The squared infinitesimal is negligible, so the increase in 
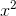was re-
ally just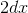 
, and we’ve really just computed the derivative of
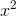with respect to 
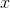and
multiplied it by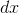 
. In symbols,
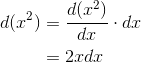
That is, the change in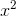 
is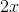 
times the change in 
. Doing
this to both sides of the original equation, we have
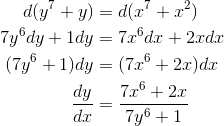
This still doesn’t give us a formula for the derivative in terms of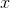 
alone, but it’s not entirely use- less. For instance, if we’re given a
numerical value of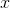 
, we can al- ways use Newton’s method to find 
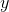, and then evaluate the derivative.
- 瀏覽次數：2086
