The fundamental theorem of calculus
Let 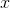 be an indefinite integral of
be an indefinite integral of 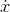 , and let
, and let 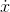 be a continuous function (one whose
graph is a single connected curve). Then
be a continuous function (one whose
graph is a single connected curve). Then
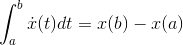
The fundamental theorem is proved in Proof of the fundamental theorem of calculus. The idea it expresses is that integration and differentiation are inverse operations. That is, integration undoes differentiation, and differentiation undoes integration.
Example
Interpret the definite integral
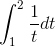
graphically; then evaluate it it both symbolically and numerically, and check that the two results are consistent.
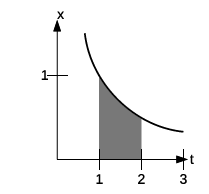
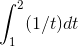
Figure 4.4 shows the graphical interpretation. The
numerical calculation requires a trivial variation on the program from Example:
a := 1; b := 2; H := 1000; dt := (b-a)/H; sum := 0; t := a; While (t<=b) [ sum := N(sum+(1/t)*dt); t := N(t+dt); ]; Echo(sum);
The result is 0.693897243, and increasing 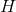 to 10,000 gives
0.6932221811, so we can be fairly confident that the result equals 0.693, to 3 decimal places.
to 10,000 gives
0.6932221811, so we can be fairly confident that the result equals 0.693, to 3 decimal places.
Symbolically, the indefinite integral is 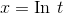 . Using the
fundamental theorem of calculus, the area is
. Using the
fundamental theorem of calculus, the area is 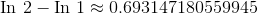 .
.
Judging from the graph, it looks plausible that the shaded area is about 0.7.
This is an interesting example, be- cause the natural log blows up to negative infinity as 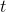 approaches 0, so it’s not possible to add a constant onto the indefinite integral and force it to be equal to 0 at
approaches 0, so it’s not possible to add a constant onto the indefinite integral and force it to be equal to 0 at 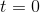 . Nevertheless, the fundamental theorem of calculus still works.
. Nevertheless, the fundamental theorem of calculus still works.
- 瀏覽次數:3210






