Actually mathematicians have invented many different logical systems for working with infinity, and in most of them infinity does come in different sizes and flavors. Newton, as well as the
German mathematician Leibniz who invented calculus independently, 1 had a strong intuitive idea that calculus was really about
numbers that were infinitely small: infinitesimals, the opposite of infinities. For instance, consider the number 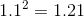 . That 2 in the first decimal place is the same 2 that appears in the expression
. That 2 in the first decimal place is the same 2 that appears in the expression 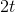 for the derivative of
for the derivative of 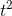 .
.
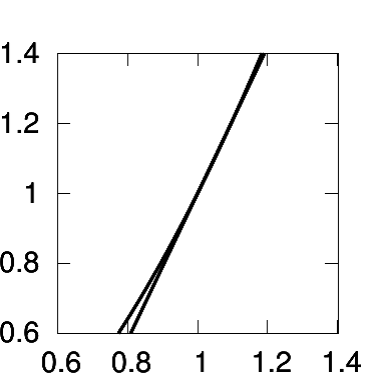
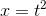 , showing the line that connects the points (1, 1) and
, showing the line that connects the points (1, 1) and
Figure 2.2shows the idea visually.
The line connecting the points (1, 1) and (1.1, 1.21) is almost indistinguishable from the tangent line on this scale. Its slope is (1.21 1)/(1.1 1) = 2.1, which is very close to the tangent
line's slope of 2. It was a good approximation because the points were close together, separated by only 0.1 on the 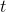 axis.
axis.
If we needed a better approximation, we could try calculating 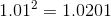 . The slope of the line connecting the points (1, 1) and (1.01, 1.0201) is 2.01, which is even closer to the slope of the tangent
line.
. The slope of the line connecting the points (1, 1) and (1.01, 1.0201) is 2.01, which is even closer to the slope of the tangent
line.
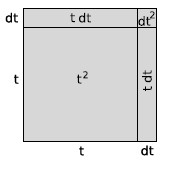
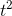
Another method of visualizing the idea is that we can interpret 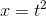 as
the area of a square with sides of length
as
the area of a square with sides of length 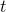 , as suggested in Figure 2.3. We increase
, as suggested in Figure 2.3. We increase 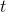 by an infinitesimally small number
by an infinitesimally small number 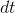 . The
. The 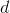 is Leibniz's notation for a very small difference, and
is Leibniz's notation for a very small difference, and 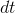 is to
be read as a single symbol, "dee-tee," not as a number
is to
be read as a single symbol, "dee-tee," not as a number 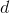 multiplied by a number
multiplied by a number 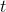 . The
idea is that
. The
idea is that 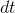 is smaller than any ordinary number you could imagine, but it's not zero.
The area of the square is increased by
is smaller than any ordinary number you could imagine, but it's not zero.
The area of the square is increased by 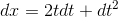 , which is analogous
to the finite numbers 0.21 and 0.0201 we calculated
earlier. Where before we divided by a finite change in
, which is analogous
to the finite numbers 0.21 and 0.0201 we calculated
earlier. Where before we divided by a finite change in 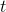 such as 0.1 or 0.01, now we divide by
such as 0.1 or 0.01, now we divide by 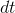 , producing
, producing
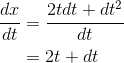
for the derivative. On a graph like Figure 2.2, 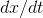 is the slope of the tangent line: the change in
is the slope of the tangent line: the change in 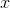 divided by the changed in
divided by the changed in 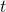 .
.
But adding an infinitesimal number 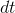 onto
onto 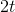 doesn't really change it by any amount that's even theoretically measurable in the real world, so the answer is really
doesn't really change it by any amount that's even theoretically measurable in the real world, so the answer is really
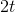 . Evaluating it at
. Evaluating it at 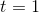 gives the exact result, 2, that the earlier approximate results, 2.1 and 2.01, were
getting closer and closer to.
gives the exact result, 2, that the earlier approximate results, 2.1 and 2.01, were
getting closer and closer to.
Example
To show the power of infinitesimals and the Leibniz notation, let’s prove that the derivative of 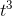 is
is 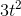 :
: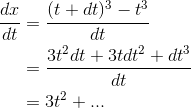
where the dots indicate infinitesimal terms that we can neglect.
This result required significant sweat and ingenuity when proved on Derivatives of polynomials by the methods of Rates of Change, and not only that but the old method would have required a completely different method of proof for a function that wasn't a polynomial, whereas the new one can be applied more generally, as we'll see presently in Example;Example;Example and Example.
It's easy to get the mistaken impression that infinitesimals exist in some remote fairyland where we can never touch them. This may be true in the same artsy-fartsy sense that we can never
truly understand 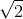 , because its decimal expansion goes on
forever, and we therefore can never compute it exactly. But in practical work, that doesn't stop us from working with
, because its decimal expansion goes on
forever, and we therefore can never compute it exactly. But in practical work, that doesn't stop us from working with 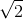 . We
just approximate it as, e.g., 1.41. Infinitesimals are no more or less mysterious than irrational numbers, and in particular we can represent them concretely on a computer. If you go to
. We
just approximate it as, e.g., 1.41. Infinitesimals are no more or less mysterious than irrational numbers, and in particular we can represent them concretely on a computer. If you go to
 , you'll find a web-based
calculator called Inf, which can handle infinite and infinitesimal numbers. It has a built-in symbol, d, which represents an infinitesimally small number such as the dx's and dt's we've been
handling symbolically.
, you'll find a web-based
calculator called Inf, which can handle infinite and infinitesimal numbers. It has a built-in symbol, d, which represents an infinitesimally small number such as the dx's and dt's we've been
handling symbolically.
Let's use Inf to verify that the derivative of 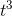 , evaluated at
, evaluated at
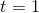 , is equal to 3, as found by plugging in to the result of Example. The : symbol is the prompt that shows you Inf is ready to
accept your typed input.
, is equal to 3, as found by plugging in to the result of Example. The : symbol is the prompt that shows you Inf is ready to
accept your typed input.
: ((1+d)^3-1)/d 3+3d+d^2
As claimed, the result is 3, or close enough to 3 that the infinitesimal error doesn't matter in real life. It might look like Inf did this example by using algebra to simplify the expression, but in fact Inf doesn't know anything about algebra. One way to see this is to use Inf to compare d with various real numbers:
: d<1 true : d<0.01 true : d<0.0000001 true : d<0 false
If d were just a variable being treated according to the axioms of algebra, there would be no way to tell how it compared with other numbers without having some special information. Inf doesn't know algebra, but it does know that d is a positive number that is less than any positive real number that can be represented using decimals or scientific notation.
Example
In Example, we made a rough numerical check to see if the
differentiation rule 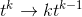 , which was proved on
Derivatives of polynomials for
, which was proved on
Derivatives of polynomials for 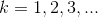 , was also valid for
, was also valid for 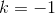 , i.e., for the function
, i.e., for the function 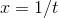 . Let’s look for an actual proof. To find a natural method of attack, let’s first redo the numerical check in a slightly
more suggestive form. Again approximating the derivating at
. Let’s look for an actual proof. To find a natural method of attack, let’s first redo the numerical check in a slightly
more suggestive form. Again approximating the derivating at 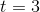 , we
have
, we
have
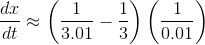
Let’s apply the grade-school technique for subtracting fractions, in which we first get them over the same denominator:
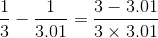
The result is
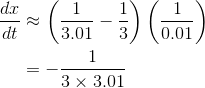
Replacing 3 with 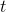 and 0.01 with
and 0.01 with 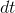 , this becomes
, this becomes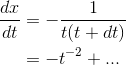
Example
The derivative of 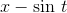 , with
, with 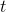 in units of radians, is
in units of radians, is
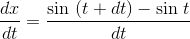
and with the trig identity 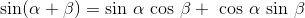 , this becomes
, this becomes
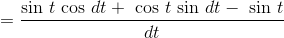
Applying the small-angle approximations 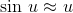 and
and 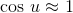 we have
we have
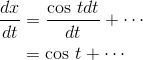
where “. . . ” represents the error caused by the small-angle
approximations.
This is essentially all there is to the computation of the
derivative, except for the remaining technical point that we haven’t proved that the small-angle approximations are good enough. In Example, when we calculated the derivative of 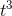 , the resulting expression for the quotient dx= dt came out in a form in which we could inspect the “. . . ” terms and verify
before discarding them that they were infinitesimal. The issue is less trivial in the present example. This point is addressed more rigorously on Details of the proof of the derivative of the sine
function
, the resulting expression for the quotient dx= dt came out in a form in which we could inspect the “. . . ” terms and verify
before discarding them that they were infinitesimal. The issue is less trivial in the present example. This point is addressed more rigorously on Details of the proof of the derivative of the sine
function
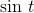 , and its derivative
, and its derivative 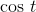 .
.
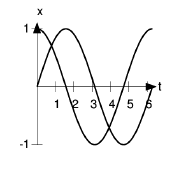
Figure 2.4 shows the graphs of the function and its derivative. Note how the two graphs correspond. At 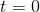 , the slope of sin t is at its largest, and is positive; this is where the
derivative, cos t, attains its maximum positive value of 1. At
, the slope of sin t is at its largest, and is positive; this is where the
derivative, cos t, attains its maximum positive value of 1. At 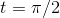 ,
, 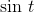 has reached a maximum, and has a slope of zero;
has reached a maximum, and has a slope of zero; 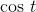 is zero here. At
is zero here. At 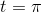 , in the middle of the graph, sin t has its maximum negative slope, and cos t is at its most negative extreme of
-1.
, in the middle of the graph, sin t has its maximum negative slope, and cos t is at its most negative extreme of
-1.
Physically, 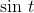 could represent the position of a pendulum as it moved back and forth
from left to right, and cos t would then be the pendulum’s velocity.
could represent the position of a pendulum as it moved back and forth
from left to right, and cos t would then be the pendulum’s velocity.
Example
What about the derivative of the cosine? The cosine and the sine are really the same function, shifted to the left or right by 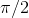 . If the derivative of the sine is the same as itself, but shifted to the left by
. If the derivative of the sine is the same as itself, but shifted to the left by 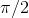 , then the derivative of the
cosine must be a cosine shifted to the left by
, then the derivative of the
cosine must be a cosine shifted to the left by 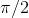 :
:
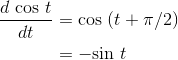
The next example will require a little trickery. By the end of this chapter you'll learn general techniques for cranking out any derivative cookbook-style, without having to come up with any tricks.
Example
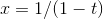
Find the derivative of 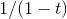 , evaluated at
, evaluated at 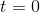 .
.
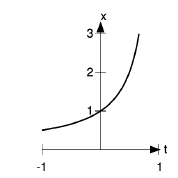
The graph shows what the function looks like. It blows up to
infinity at 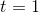 , but it’s well behaved at
, but it’s well behaved at 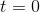 , where it has a positive slope.
, where it has a positive slope.
For insight, let’s calculate some points on the curve. The
point at which we’re differentiating is (0, 1). If we put in a small, positive value of 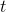 , we can observe how much the result increases relative to 1, and this will give us an approximation to the
derivative. For example, we find that at
, we can observe how much the result increases relative to 1, and this will give us an approximation to the
derivative. For example, we find that at 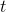 = 0.001, the function has the value 1.001001001001, and so the derivative is approximately (1.0011)/(.001-0), or
about 1. We can therefore conjecture that the derivative is exactly 1, but that’s not the same as proving it.
= 0.001, the function has the value 1.001001001001, and so the derivative is approximately (1.0011)/(.001-0), or
about 1. We can therefore conjecture that the derivative is exactly 1, but that’s not the same as proving it.
But let’s take another look at that number 1.001001001001.
It’s clearly a repeating decimal. In other words, it appears that
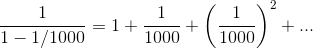
and we can easily verify this by multiplying both sides of
the equation by 1-1/1000 and collecting like powers. This is a special case of the geometric series
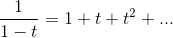 which can be derived 2 by doing synthetic division (the equivalent of long
division for polynomials), or simply verified, after forming the conjecture based on the numerical example above, by multiplying both sides by 1-t.
which can be derived 2 by doing synthetic division (the equivalent of long
division for polynomials), or simply verified, after forming the conjecture based on the numerical example above, by multiplying both sides by 1-t.
As we’ll see in Safe use of infinitesimals, and have been implicitly assuming so far, infinitesimals obey
all the same elementary laws of algebra as the real numbers, so the above derivation also holds for an infinitesimal value of 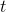 . We can verify the result using
Inf:
. We can verify the result using
Inf:
: 1/(1-d) 1+d+d^2+d^3+d^4
Notice, however, that the series is truncated after the first
five terms. This is similar to the truncation that happens when you ask your calculator to find 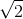 as a decimal.
as a decimal.
The result for the derivative is
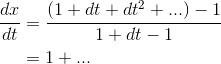
- 瀏覽次數:3641






