That proves that 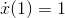 , but it was a lot of work, and we don't
want to do that much work to evaluate
, but it was a lot of work, and we don't
want to do that much work to evaluate 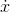 at every value of
at every value of
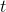 . There's a way to avoid all that, and find a formula for
. There's a way to avoid all that, and find a formula for 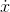 . Compare Figure 1.8 and Figure 1.10. They're both graphs of the same function, and they both look the
same. What's different? The only difference is the scales: in Figure 1.10, the
. Compare Figure 1.8 and Figure 1.10. They're both graphs of the same function, and they both look the
same. What's different? The only difference is the scales: in Figure 1.10, the 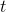 axis has been shrunk by a factor of 2, and the
axis has been shrunk by a factor of 2, and the 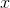 axis by a factor of 4. The graph looks the same, because doubling
axis by a factor of 4. The graph looks the same, because doubling 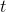 quadruples
quadruples 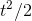 . The tangent line here is the tangent line at
. The tangent line here is the tangent line at 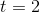 , not
, not 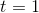 , and although it looks like the same line as the one in Figure 1.8, it isn't, because the scales are different. The line in Figure 1.8 had a slope of rise/run = 1/1 = 1, but this one's slope is 4/2 = 2. That means
, and although it looks like the same line as the one in Figure 1.8, it isn't, because the scales are different. The line in Figure 1.8 had a slope of rise/run = 1/1 = 1, but this one's slope is 4/2 = 2. That means 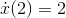 . In general, this scaling argument shows that
. In general, this scaling argument shows that 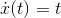 for any
for any  .
.
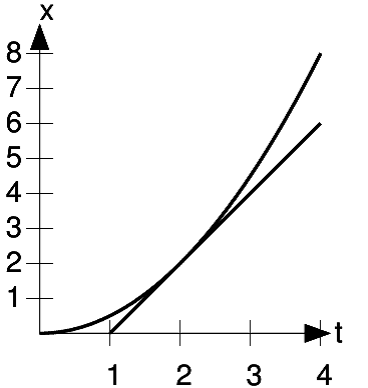
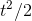 again. How is this different from Figure 1.8?
again. How is this different from Figure 1.8?
This is called differentiating: finding a formula for the function 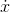 , given a formula for the function
, given a formula for the function 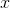 . The term comes from the idea that for a discrete function, the slope is the difference between two successive values of the
function.
. The term comes from the idea that for a discrete function, the slope is the difference between two successive values of the
function.
The function 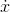 is referred to as the derivative of the function
is referred to as the derivative of the function 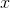 , and the art of differentiating is differential calculus. The opposite
process, computing a formula for
, and the art of differentiating is differential calculus. The opposite
process, computing a formula for 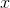 when given
when given 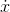 ,
is called integrating, and makes up the field of integral calculus; this terminology is based on the idea that computing a running sum is like putting together (integrating) many little pieces.
,
is called integrating, and makes up the field of integral calculus; this terminology is based on the idea that computing a running sum is like putting together (integrating) many little pieces.
Note the similarity between this result for continuous functions,
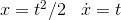
and our earlier result for discrete ones,
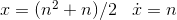
The similarity is no coincidence. A continuous function is just a smoothed-out version of a discrete one. For instance, the continuous version of the staircase function shown in Figure 1.2 would simply be a triangle
without the saw teeth sticking out; the area of those ugly sawteeth is what's represented by the 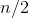 term in the discrete result
term in the discrete result 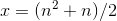 , which is the only thing that makes it different from the continuous result
, which is the only thing that makes it different from the continuous result 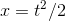 .
.
- 瀏覽次數:2185






