Available under Creative Commons-ShareAlike 4.0 International License.
In free fall, the acceleration will not be exactly constant, due to
air resistance. For example, a skydiver does not speed up indefinitely until opening her chute, but rather approaches a certain maximum velocity at which the upward force of air resistance
cancels out the force of gravity. The expression for the distance dropped by of a free-falling object, with air resistance, is 1 ![d=A \textrm{ In}\left [ \textrm{cosh}\left ( \sqrt[t]{\frac{g}{A}} \right ) \right ]](/system/files/resource/33/33298/34219/media/eqn-img_76.gif)
where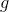 
is
the acceleration the object would have without air resistance, the function cosh has been defined in Problem 2.17,
and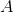 
is a constant that depends on the size, shape, and mass of the object, and
the density of the air. (For a sphere of mass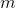 
and diameter 
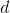dropping in air, 
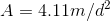. Cf. Problem 2.10)
- (a) Differentiate this expression to find the velocity. Hint: In order to simplify the writing, start by defining some other symbol to stand for the constant
.
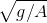- (b) Show that your answer can be reexpressed in terms of the function tanh defined by tanh
.
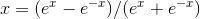- (c) Show that your result for the velocity approaches a constant for large values of
.
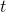- (d) Check that your answers to parts b and c have units of velocity.
- 瀏覽次數：1984
