The definition of the limit in terms of infinitesimals extends immediately to limiting processes where x gets bigger and bigger, rather than closer and closer to some finite value. For example,
the function 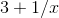 clearly gets closer and closer to 3 as
clearly gets closer and closer to 3 as 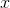 gets bigger and bigger. If
gets bigger and bigger. If  is an infinite number, then the definition says that evaluating this expression at
is an infinite number, then the definition says that evaluating this expression at 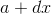 , where
, where 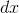 is infinitesimal, gives a result whose standard part is 3. It doesn’t matter that
is infinitesimal, gives a result whose standard part is 3. It doesn’t matter that  happens to be infinite, the definition still works. We also note that in this example, it
doesn’t matter what infinite number
happens to be infinite, the definition still works. We also note that in this example, it
doesn’t matter what infinite number  is; the limit equals 3 for any infinite
is; the limit equals 3 for any infinite  . We can write this fact as
. We can write this fact as
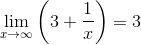
where the symbol 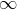 is to be interpreted as “nyeah nyeah, I don’t
even care what infinite number you put in here, I claim it will work out to 3 no matter what.” The symbol
is to be interpreted as “nyeah nyeah, I don’t
even care what infinite number you put in here, I claim it will work out to 3 no matter what.” The symbol 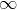 is not to
be interpreted as standing for any specific infinite number. That would be the type of fallacy that lay behind the bogus proof in Safe use of infinitesimals that 1 = 1/2, which assumed that all infinities had to be the same
size.
is not to
be interpreted as standing for any specific infinite number. That would be the type of fallacy that lay behind the bogus proof in Safe use of infinitesimals that 1 = 1/2, which assumed that all infinities had to be the same
size.
A somewhat different example is the arctangent function. The arctangent of 1000 equals approximately 1.5698, and inputting bigger and bigger numbers gives answers that appear to get closer and
closer to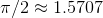 . But the arctangent of -1000 is
approximately -1.5698, i.e., very close to
. But the arctangent of -1000 is
approximately -1.5698, i.e., very close to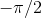 . From these numerical
observations, we conjecture that
. From these numerical
observations, we conjecture that
equals 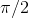 for positive infinite
for positive infinite  , but
, but 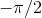 for
negative infinite
for
negative infinite  . It would not be correct to write
. It would not be correct to write
![\begin{matrix} \lim_{x\rightarrow \infty} \textrm{tan}^{-1}x=\frac{\pi}{2} & \textrm{[wrong]} \end{matrix}](/system/files/resource/33/33298/33538/media/eqn-img_19.gif)
because it does matter what infinite number we pick. Instead we write
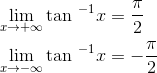
Some expressions don't have this kind of limit at all. For example, if you take the sines of big numbers like a thousand, a million, etc., on your calculator, the results are essentially random
numbers lying between 1 and 1. They don't settle down to any particular value, because the sine function oscillates back and forth forever. To prove formally that 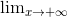
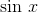 is undefined, consider that the sine function, defined on the real numbers, has the
property that you can always change its result by at least 0.1 if you add either 1.5 or 1.5 to its input. For example,
is undefined, consider that the sine function, defined on the real numbers, has the
property that you can always change its result by at least 0.1 if you add either 1.5 or 1.5 to its input. For example, 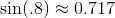 , and
, and 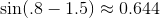 . Applying the transfer principle to this statement, we find that the same is true on the
hyperreals. Therefore there cannot be any value l that differs infinitesimally from
. Applying the transfer principle to this statement, we find that the same is true on the
hyperreals. Therefore there cannot be any value l that differs infinitesimally from 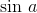 for all positive infinite values of
for all positive infinite values of  .
.
Often we're interested in finding the limit as 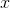 approaches infinity of
an expression that is written as an indeterminate form like
approaches infinity of
an expression that is written as an indeterminate form like 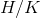 , where
both
, where
both 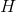 and
and 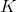 are infinite.
are infinite.
Example
Evaluate the limit
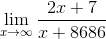
Intuitively, if 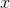 gets large enough the constant terms will be
negligible, and the top and bottom will be dominated by the
gets large enough the constant terms will be
negligible, and the top and bottom will be dominated by the 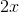 and
and
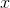 terms, respectively, giving an answer that approaches 2.
terms, respectively, giving an answer that approaches 2.
One way to verify this is to divide both the top and the bottom by 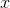 , giving
, giving
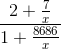
If x is infinite, then the standard part of the top is 2, the standard part of the bottom is 1, and the standard part of the whole thing is therefore 2.
Another approach is to use l’Hopital’s rule. The derivative of the top is 2, and the derivative of the bottom is 1, so the limit is 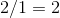 .
.
- 瀏覽次數:3514






