Change of variable

Available under Creative Commons-ShareAlike 4.0 International License.

We will build up the rest of the features of l’Hˆopital’s rule using the technique of a change of variable. To demonstrate how this works, let’s imagine that we were starting from an even more stripped-down version of l’Hˆopital’s rule than the one on p. 61. Say we only knew how to do limits of the form x→0 rather than x→afor an arbitrary real number a. We could then evaluate 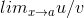$lim_{x\rightarrow a}u/v$ simply by defining t = x−a and reexpressing u and v in terms of t.

Example 104

Reduce
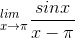
$_{x\rightarrow \pi }^{lim}\frac{sin x}{x-\pi }$
to a form involving a limit at 0.

x→π x−π

.Define t= x−π. Solving for xgives x= t+ π. We substitute into the above expression to find

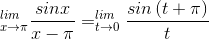$_{x\rightarrow \pi }^{lim}\frac{sin x}{x-\pi }=_{t\rightarrow 0}^{lim}\frac{sin\left ( t+\pi \right )}{t}$ If all we knew was the →0 form of l’Hoˆ pital’s rule, then this would suffice to reduce the problem to one we knew how to solve. In fact, this kind of change of variable works in all cases, not just for a limit at π, so rather then going through a laborious change of variable every time, we could simply establish the more general form on p. 61, with →a.

瀏覽次數：1960

您在這裡

Change of variable

Example 104