Available under Creative Commons-ShareAlike 4.0 International License.
Suppose that we’ve already established that the derivative of an odd function is even, and vice versa. (See Problem 2.30) Something similar can be proved for integration. However, the
following is not quite right. Let 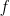 be even, and
let
be even, and
let 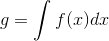 be its indefinite integral. Then by the
fundamental theorem of calculus,
be its indefinite integral. Then by the
fundamental theorem of calculus, 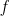 is the derivative of
is the derivative of 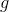 . Since we’ve already established that the derivative of an odd function is even, we conclude that
. Since we’ve already established that the derivative of an odd function is even, we conclude that 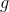 is odd. Find all errors in the proof.
is odd. Find all errors in the proof.
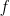 be even, and
let
be even, and
let 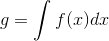 be its indefinite integral. Then by the
fundamental theorem of calculus,
be its indefinite integral. Then by the
fundamental theorem of calculus, 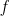 is the derivative of
is the derivative of 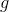 . Since we’ve already established that the derivative of an odd function is even, we conclude that
. Since we’ve already established that the derivative of an odd function is even, we conclude that 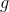 is odd. Find all errors in the proof.
is odd. Find all errors in the proof.
- 瀏覽次數:2498






