The natural logarithm is the function that undoes the exponential. In a situation like this, we have
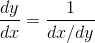
where on the left we're thinking of 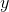 as a function of
as a function of 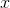 , and on the right we consider
, and on the right we consider 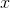 to be a function of
to be a function of 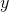 .
Applying this to the natural logarithm,
.
Applying this to the natural logarithm,
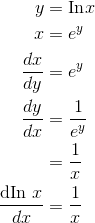
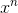 . Constants out in front of the functions are not
shown, so keep in mind that, for example, the derivative of
. Constants out in front of the functions are not
shown, so keep in mind that, for example, the derivative of 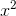 isn’t
isn’t 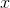 , it’s 2
, it’s 2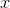 .
.
This is noteworthy because it shows that there must be an exception to the rule that the derivative of 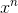 is
is
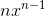 , and the integral of
, and the integral of 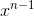 is
is 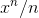 . (In The chain rule I remarked that this rule could be proved using the product rule for negative integer values of
. (In The chain rule I remarked that this rule could be proved using the product rule for negative integer values of 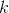 , but that I would give a simpler, less tricky, and more general proof later. The proof is Example below.) The integral of
, but that I would give a simpler, less tricky, and more general proof later. The proof is Example below.) The integral of 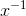 is not
is not 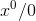 , which wouldn't make sense anyway because it involves division by zero. 1 Likewise the derivative of
, which wouldn't make sense anyway because it involves division by zero. 1 Likewise the derivative of 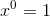 is
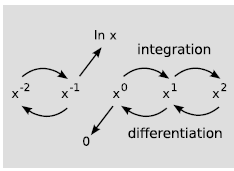
is 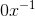 , which is zero. Figure 2.12 shows the idea. The functions xn form a kind of ladder, with
differentiation taking us down one rung, and integration taking us up. However, there are two special cases where differentiation takes us of the ladder entirely.
, which is zero. Figure 2.12 shows the idea. The functions xn form a kind of ladder, with
differentiation taking us down one rung, and integration taking us up. However, there are two special cases where differentiation takes us of the ladder entirely.
Example
Prove 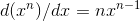 for any real value of
for any real value of 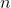 , not just an integer.
, not just an integer.
By the chain rule,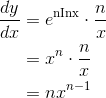
(For 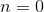 , the result is zero.)
, the result is zero.)
When I started the discussion of the derivative of the logarithm, I wrote 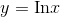 right of the bat. That meant I was implicitly assuming
right of the bat. That meant I was implicitly assuming 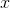 was positive. More generally, the derivative of
was positive. More generally, the derivative of 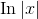 equals
equals 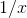 , regardless of the sign (see Problem 2.29 ).
, regardless of the sign (see Problem 2.29 ).
- 瀏覽次數:3338






